河北省唐山市乐亭县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-28 类型:期末考试
一、单选题
-
1. 为了解我校初三年级所有同学的数学成绩,从中抽出500名同学的数学成绩进行调查,抽出的500名考生的数学成绩是( )A、总体 B、样本 C、个体 D、样本容量2. 在一次数学测试中,将某班50名学生的成绩分为5组,第一组到第四组的频率之和为0.8,则第5组的频数是( )A、10 B、9 C、8 D、73. 如图,将□ABCD的一边BC延长至点E , 若∠A=110°,则∠1等于( )
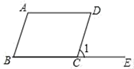 A、110° B、35° C、70° D、55°4. 课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成( )
A、110° B、35° C、70° D、55°4. 课间操时,小明、小丽、小亮的位置如图所示,小明对小亮说:如果我的位置用(0,0)表示,小丽的位置用(2,1)表示,那么你的位置可以表示成( ) A、(5,4) B、(4,5) C、(3,4) D、(4,3)5. 点P在第四象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )A、(-4,3) B、(-3,4) C、(4,-3) D、(3,-4)6. 一次函数y=x+4的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若 A( , )、B( , )是一次函数 y=(a-1)x+2 图象上的不同的两个点,当 > 时, < ,则 a 的取值范围是( )A、a>0 B、a<0 C、a>1 D、a<18. 如图,将点P(-1,3)向右平移n个单位后落在直线y=2x-1上的点P′处,则n等于( )
A、(5,4) B、(4,5) C、(3,4) D、(4,3)5. 点P在第四象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标为( )A、(-4,3) B、(-3,4) C、(4,-3) D、(3,-4)6. 一次函数y=x+4的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若 A( , )、B( , )是一次函数 y=(a-1)x+2 图象上的不同的两个点,当 > 时, < ,则 a 的取值范围是( )A、a>0 B、a<0 C、a>1 D、a<18. 如图,将点P(-1,3)向右平移n个单位后落在直线y=2x-1上的点P′处,则n等于( )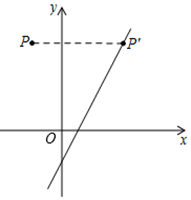 A、2 B、 C、3 D、49. 如图,在矩形 中,对角线 相交于点 ,且 ,则图中长度为3的线段有( )
A、2 B、 C、3 D、49. 如图,在矩形 中,对角线 相交于点 ,且 ,则图中长度为3的线段有( ) A、2条 B、4条 C、5条 D、6条10. 菱形 在平面直角坐标系中的位置如图所示,点C的坐标是
A、2条 B、4条 C、5条 D、6条10. 菱形 在平面直角坐标系中的位置如图所示,点C的坐标是 ,点A的纵坐标是
,点A的纵坐标是  ,则点B的坐标是( )
,则点B的坐标是( )  A、
A、 B、
B、 C、
C、 D、
D、 11. 某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
11. 某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )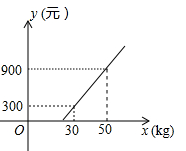 A、20kg B、25kg C、28kg D、30kg12. 如图,过正五边形 的顶点 作直线 ,则 的度数为( )
A、20kg B、25kg C、28kg D、30kg12. 如图,过正五边形 的顶点 作直线 ,则 的度数为( ) A、 B、 C、 D、13. 如图,证明矩形的对角线相等,已知:四边形 是矩形.求证: .以下是排乱了的证明过程:①∴ 、 .②∵ ③∵四边形 是矩形④∴ ⑤∴ .证明步骤正确的顺序是( )
A、 B、 C、 D、13. 如图,证明矩形的对角线相等,已知:四边形 是矩形.求证: .以下是排乱了的证明过程:①∴ 、 .②∵ ③∵四边形 是矩形④∴ ⑤∴ .证明步骤正确的顺序是( ) A、③①②⑤④ B、②①③⑤④ C、③⑤②①④ D、②⑤①③④14. 已知一次函数的图象过点(0,3),且与两坐标轴围成的三角形的面积为3,则这个一次函数的表达式为( )A、y=1.5x+3 B、y=-1.5x+3 C、y=1.5x+3或y=-1.5x+3 D、y=1.5x-3或y=-1.5x-315. 如图,点 是矩形 的对角线 的中点, 是 边的中点,若 ,则 的长为( )
A、③①②⑤④ B、②①③⑤④ C、③⑤②①④ D、②⑤①③④14. 已知一次函数的图象过点(0,3),且与两坐标轴围成的三角形的面积为3,则这个一次函数的表达式为( )A、y=1.5x+3 B、y=-1.5x+3 C、y=1.5x+3或y=-1.5x+3 D、y=1.5x-3或y=-1.5x-315. 如图,点 是矩形 的对角线 的中点, 是 边的中点,若 ,则 的长为( ) A、5 B、6 C、8 D、1016. 如图,正比例函数 的图象与一次函数 的图象交于点 ,若点 是直线 上的一个动点,则线段 长的最小值为( )
A、5 B、6 C、8 D、1016. 如图,正比例函数 的图象与一次函数 的图象交于点 ,若点 是直线 上的一个动点,则线段 长的最小值为( ) A、1 B、 C、 D、2
A、1 B、 C、 D、2二、填空题
-
17. 内角和等于外角和2倍的多边形是边形.18. 已知函数 ,当 时,函数值 为 .19. 如图,过正方形 的顶点 作直线 ,过 作 的垂线,垂足分别为 .若 , ,则 的长度为 .
 20. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB= ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为 .
20. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB= ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为 .
三、解答题
-
21. 某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为 四个等级,绘制了图①、图②两幅不完整的统计图,请结合图中所给信息解答下列问题:
 (1)、求本次抽查的学生共有人;(2)、将条形统计图和扇形统计图补充完整;(3)、扇形统计图中“ ”所在扇形圆心角的度数为;(4)、估计全校“ ”等级的学生有人22. 长方形 放置在如图所示的平面直角坐标系中,点 轴, 轴, .
(1)、求本次抽查的学生共有人;(2)、将条形统计图和扇形统计图补充完整;(3)、扇形统计图中“ ”所在扇形圆心角的度数为;(4)、估计全校“ ”等级的学生有人22. 长方形 放置在如图所示的平面直角坐标系中,点 轴, 轴, . (1)、分别写出点 的坐标;; .(2)、在 轴上是否存在点 ,使三角形 的面积为长方形ABCD面积的 ?若存在,请直接写出点 的坐标;若不存在,请说明理由.23. 如图,直线 与直线 交于点 ,直线 经过点 .
(1)、分别写出点 的坐标;; .(2)、在 轴上是否存在点 ,使三角形 的面积为长方形ABCD面积的 ?若存在,请直接写出点 的坐标;若不存在,请说明理由.23. 如图,直线 与直线 交于点 ,直线 经过点 . (1)、求直线 的函数表达式;(2)、直接写出方程组 的解;(3)、若点 在直线 的下方,直线 的上方,写出 的取值范围 .24. 如图,在Rt△ABC中,∠ACB=90,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE
(1)、求直线 的函数表达式;(2)、直接写出方程组 的解;(3)、若点 在直线 的下方,直线 的上方,写出 的取值范围 .24. 如图,在Rt△ABC中,∠ACB=90,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE (1)、求证:CE=AD(2)、当点D在AB中点时,四边形BECD是什么特殊四边形?说明理由(3)、若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?说明理由.25. 甲、乙两人在笔直的道路 上相向而行,甲骑自行车从 地到 地,乙驾车从 地到 地,假设他们分别以不同的速度匀速行驶,甲先出6分钟后,乙才出发,乙的速度为 千米/分,在整个过程中,甲、乙两人之间的距离 (千米)与甲出发的时间 (分)之间的部分函数图象如图.
(1)、求证:CE=AD(2)、当点D在AB中点时,四边形BECD是什么特殊四边形?说明理由(3)、若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?说明理由.25. 甲、乙两人在笔直的道路 上相向而行,甲骑自行车从 地到 地,乙驾车从 地到 地,假设他们分别以不同的速度匀速行驶,甲先出6分钟后,乙才出发,乙的速度为 千米/分,在整个过程中,甲、乙两人之间的距离 (千米)与甲出发的时间 (分)之间的部分函数图象如图. (1)、 两地相距千米,甲的速度为千米/分;(2)、直接写出点 的坐标 , 求线段 所表示的 与 之间的函数表达式;(3)、当乙到达终点 时,甲还需分钟到达终点 .26.
(1)、 两地相距千米,甲的速度为千米/分;(2)、直接写出点 的坐标 , 求线段 所表示的 与 之间的函数表达式;(3)、当乙到达终点 时,甲还需分钟到达终点 .26. (1)、操作思考:如图1,在平面直角坐标系中,等腰直角 的直角顶点 在原点,将其绕着点 旋转,若顶点 恰好落在点 处.则① 的长为;②点 的坐标为(直接写结果)(2)、感悟应用:如图2,在平面直角坐标系中,将等腰直角 如图放置,直角顶点 ,点 ,试求直线 的函数表达式.(3)、拓展研究:如图3,在直角坐标系中,点 ,过点 作 轴,垂足为点 ,作 轴,垂足为点 是线段 上的一个动点,点 是直线 上一动点.问是否存在以点 为直角顶点的等腰直角 ,若存在,请直接写出此时 点的坐标,若不存在,请说明理由.
(1)、操作思考:如图1,在平面直角坐标系中,等腰直角 的直角顶点 在原点,将其绕着点 旋转,若顶点 恰好落在点 处.则① 的长为;②点 的坐标为(直接写结果)(2)、感悟应用:如图2,在平面直角坐标系中,将等腰直角 如图放置,直角顶点 ,点 ,试求直线 的函数表达式.(3)、拓展研究:如图3,在直角坐标系中,点 ,过点 作 轴,垂足为点 ,作 轴,垂足为点 是线段 上的一个动点,点 是直线 上一动点.问是否存在以点 为直角顶点的等腰直角 ,若存在,请直接写出此时 点的坐标,若不存在,请说明理由.