河北省石家庄市正定县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-28 类型:期末考试
一、单选题
-
1. 在函数y= 中,自变量x的取值范围是( )A、x>1 B、x<1 C、x≠1 D、x=1
-
2. 为了了解2019年石家庄市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩。下列说法正确的是( )A、2019年石家庄市九年级学生是总体 B、每一名九年级学生是个体 C、1000名九年级学生是总体的一个样本 D、样本容量是1000
-
3. 如图,被笑脸盖住的点的坐标可能是( )
 A、(3,2) B、(-3,2) C、(-3,-2) D、(3,-2)
A、(3,2) B、(-3,2) C、(-3,-2) D、(3,-2) -
4. 如图,要测量被池塘隔开的A、C两点间的距离,李师傅在AC外任选一点B,连接BA和BC,分别取BA和BC的中点E、F,量得EF两点间距离等于23米,则A、C两点间的距离为( )米
 A、23 B、46 C、50 D、2
A、23 B、46 C、50 D、2 -
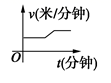
5. 某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进达到学校.小明走路的速度v(米/分钟)是时间t(分钟)的函数,能符合题意反映这一函数关系的大致图像是( )A、
 B、
B、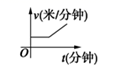 C、
C、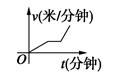 D、
D、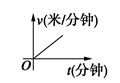
-
6. 某种正方形合金板材的成本y(元)与它的面积成正比,设边长为xcm.当x=3时,y=18,那么当成本为72元时,边长为( )A、6cm B、12cm C、24cm D、36cm
-
7. 某平行四边形的对角线长为x,y,一边长为6,则x与y的值可能是( )A、4和7 B、5和7 C、5和8 D、4和17
-
8. 如图,已知一次函数y=ax+b和y=kx的图象相交于点P,则根据图象可得二元一次方程组 的解是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
9. 下列命题中正确的是( )A、有一组邻边相等的四边形是菱形 B、有一个角是直角的平行四边形是矩形 C、对角线垂直的平行四边形是正方形 D、一组对边平行的四边形是平行四边形
-
10. 已知一次函数y=kx+b﹣x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )A、k>1, B、 , C、 , D、 ,
-
11. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )
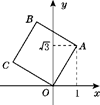 A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)
A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1) -
12. 如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,……,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
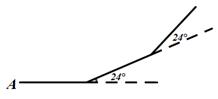 A、140米 B、150米 C、160米 D、240米
A、140米 B、150米 C、160米 D、240米 -
13. 在平面直角坐标系中,点 在第一象限,若点 关于 轴的对称点 在直线 上,则 的值为( )A、3 B、2 C、1 D、-1
-
14. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )
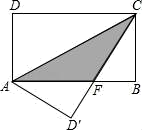 A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12 -
15. 如图,直线l:y=- x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
 A、1<a<2 B、-2<a<0 C、-3≤a≤-2 D、-10<a<-4
A、1<a<2 B、-2<a<0 C、-3≤a≤-2 D、-10<a<-4 -
16. 如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100m,则小聪行走的路程为( )m.
 A、3100 B、4600 C、3000 D、3600
A、3100 B、4600 C、3000 D、3600
二、填空题
-
17. 已知点(-4,y1),(2,y2)都在直线y=ax+2(a<0)上,则y1 , y2的大小关系为 .
-
18. 如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC上点P的坐标为(a,b),那么点P变换后的对应点P′的坐标为 .

-
19. 如图,矩形ABOC的顶点A的坐标为(﹣4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是 .

-
20. 如图,矩形 的面积为20cm2 , 对角线交于点 ,以AB、AO为邻边作平行四边形 ,对角线交于点 ;以 为邻边作平行四边形 ;…;依此类推,则平行四边形 的面积为 , 平行四边形 的面积为.

三、解答题
-
21. 随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到图表(部分信息未给出):


根据以上信息解答下列问题:
(1)、这次被调查的学生有多少人?(2)、求表中m,n,p的值,并补全条形统计图.(3)、若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议. -
22. 甲、乙两列火车分别从A、B两城同时匀速驶出,甲车开往B城,乙车开往A城.由于墨迹遮盖,图中提供的是两车距B城的路程S甲(千米)、S乙(千米)与行驶时间t(时)的函数图象的一部分.
 (1)、分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);(2)、求A、B两城之间的距离,及t为何值时两车相遇;(3)、当两车相距300千米时,求t的值.
(1)、分别求出S甲、S乙与t的函数关系式(不必写出t的取值范围);(2)、求A、B两城之间的距离,及t为何值时两车相遇;(3)、当两车相距300千米时,求t的值. -
23. 如图1,在△ABC中,按如下步骤作图:①以点A为圆心,AB长为半径画弧;②以点C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD.
 (1)、填空:△ABC≌△;AC和BD的位置关系是(2)、如图2,当AB=BC时,猜想四边形ABCD是什么四边形,并证明你的结论.(3)、在(2)的条件下,若AC=8cm,BD=6cm,则点B到AD的距离是cm,若将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长为cm.
(1)、填空:△ABC≌△;AC和BD的位置关系是(2)、如图2,当AB=BC时,猜想四边形ABCD是什么四边形,并证明你的结论.(3)、在(2)的条件下,若AC=8cm,BD=6cm,则点B到AD的距离是cm,若将四边形ABCD通过割补,拼成一个正方形,那么这个正方形的边长为cm. -
24. 某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)(1)、一名熟练工加工1件A型服装和1件B型服装各需要多少小时?(2)、一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
-
25. 已知直线y=kx+3(1-k)(其中k为常数,k≠0),k取不同数值时,可得不同直线,请探究这些直线的共同特征.

实践操作
(1)、当k=1时,直线l1的解析式为 , 请在图1中画出图象;当k=2时,直线l2的解析式为 , 请在图2中画出图象;(2)、探索发现直线y=kx+3(1-k)必经过点( , );
(3)、类比迁移矩形ABCD如图2所示,若直线y=kx+k-2(k≠0)分矩形ABCD的面积为相等的两部分,请在图中直接画出这条直线.
-
26.
如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,
 (1)、求∠EAF的度数;(2)、在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2;(3)、在图②中,若AG=12, BM= ,直接写出MN的值.
(1)、求∠EAF的度数;(2)、在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2;(3)、在图②中,若AG=12, BM= ,直接写出MN的值.
