河北省石家庄市新乐市2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-28 类型:期末考试
一、单选题
-
1. 下列调查中,适合进行普查的是( )A、一个班级学生的体重 B、我国中学生喜欢上数学课的人数 C、一批灯泡的使用寿命 D、《新闻联播》电视栏目的收视率2. 在平面直角坐标系中,点P(-2,x2+1)所在的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 一次函数y=x+2的图象与x轴的交点坐标为( )
A、(0,2) B、(0,﹣2) C、(2,0) D、(﹣2,0)4. 小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点P的坐标表示正确的是( ) A、(5,30) B、(8,10) C、(9,10) D、(10,10)5. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果
A、(5,30) B、(8,10) C、(9,10) D、(10,10)5. 如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果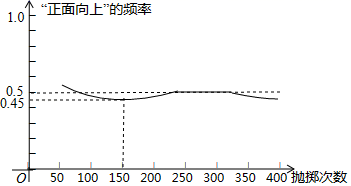
下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A、① B、② C、①② D、①③6. 下列命题不正确的是( )A、对角线互相垂直平分的四边形是菱形 B、平行四边形的对角线互相平分 C、矩形的对角线相等 D、对角线相等的四边形是矩形7. 如图,在矩形AOBC中,A(–2,0),B(0,1).若正比例函数y=kx的图象经过点C,则k的值为( ) A、– B、 C、–2 D、28. 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
A、– B、 C、–2 D、28. 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )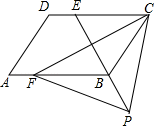 A、1 B、2 C、3 D、49. 图中两直线L1 , L2的交点坐标可以看作方程组( )的解.
A、1 B、2 C、3 D、49. 图中两直线L1 , L2的交点坐标可以看作方程组( )的解. A、 B、 C、 D、10. 如图,点 是菱形 边上的一动点,它从点 出发沿在 路径匀速运动到点 ,设 的面积为 , 点的运动时间为 ,则 关于 的函数图象大致为
A、 B、 C、 D、10. 如图,点 是菱形 边上的一动点,它从点 出发沿在 路径匀速运动到点 ,设 的面积为 , 点的运动时间为 ,则 关于 的函数图象大致为 A、
A、 B、
B、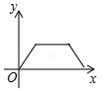 C、
C、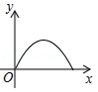 D、
D、
二、填空题
-
11. 平面直角坐标系中,将点A(1,﹣2)向上平移1个单位长度后与点B重合,则点B的坐标是 .12. 某学校为了解本校学生课外阅读的情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成统计表,如下表.已知该校学生人数为1200人,由此可以估计每周课外阅读时间在1~2(不含1)小时的学生有人.
每周课外阅读时间(小时)
0~1
1~2(不含1)
2~3(不含2)
超过3
人 数
7
10
14
19
13. 函数y= 中自变量x的取值范围是 .14. 如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .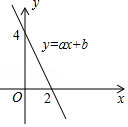 15. 如图,在矩形ABCD中,顺次连接矩形四边的中点得到四边形EFGH.若AB=8,AD=6,则四边形EFGH的周长等于 .
15. 如图,在矩形ABCD中,顺次连接矩形四边的中点得到四边形EFGH.若AB=8,AD=6,则四边形EFGH的周长等于 . 16. 如图,在平行四边形ABCD中,AB=4,BC=6,分别以A,C为圆心,以大于 AC的长为半径作弧,两弧相交于MN两点,作直线MN交AD于点E,则△CDE的周长是 .
16. 如图,在平行四边形ABCD中,AB=4,BC=6,分别以A,C为圆心,以大于 AC的长为半径作弧,两弧相交于MN两点,作直线MN交AD于点E,则△CDE的周长是 .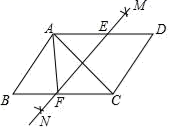 17. 如图,在平面直角坐标系中,点M是直线y=﹣x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为 .
17. 如图,在平面直角坐标系中,点M是直线y=﹣x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤8时,设点M的横坐标为m,则m的取值范围为 .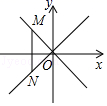 18. 根据如图所示的程序计算函数y的值,若输入的x值是4或7时,输出的y值相等,则b等于
18. 根据如图所示的程序计算函数y的值,若输入的x值是4或7时,输出的y值相等,则b等于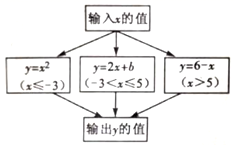
三、解答题
-
19. 如图,小亮从点 处出发,前进5米后向右转 ,再前进5米后又向右转 ,这样走 次后恰好回到出发点 处.
 (1)、小亮走出的这个 边形的每个内角是多少度?这个 边形的内角和是多少度?(2)、小亮走出的这个 边形的周长是多少米?20. 已知:如图,在四边形 中, , 为对角线 的中点, 为 的中点, 为 的中点.求证:
(1)、小亮走出的这个 边形的每个内角是多少度?这个 边形的内角和是多少度?(2)、小亮走出的这个 边形的周长是多少米?20. 已知:如图,在四边形 中, , 为对角线 的中点, 为 的中点, 为 的中点.求证: 21. 如图, 是边长为 的等边三角形.
21. 如图, 是边长为 的等边三角形. (1)、求 边上的高 与 之间的函数关系式。 是 的一次函数吗?如果是一次函数,请指出相应的 与 的值.(2)、当 时,求 的值.(3)、求 的面积 与 之间的函数关系式. 是 的一次函数吗?22. 如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
(1)、求 边上的高 与 之间的函数关系式。 是 的一次函数吗?如果是一次函数,请指出相应的 与 的值.(2)、当 时,求 的值.(3)、求 的面积 与 之间的函数关系式. 是 的一次函数吗?22. 如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.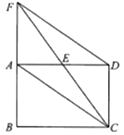 (1)、求证:四边形ACDF是平行四边形;(2)、当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.23. 某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
(1)、求证:四边形ACDF是平行四边形;(2)、当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.23. 某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图. (1)、这次被调查的同学共有人;(2)、补全条形统计图,并在图上标明相应的数据;(3)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
(1)、这次被调查的同学共有人;(2)、补全条形统计图,并在图上标明相应的数据;(3)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.