河北省秦皇岛市卢龙县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-05-28 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 为了解我市参加中考的15 000名学生的视力情况，抽查了1 000名学生的视力进行统计分析，下面四个判断正确的是（    ）
    A、15000名学生是总体 B、1000名学生的视力是总体的一个样本 C、每名学生是总体的一个个体 D、以上调查是普查

    查看试题解析

  • 2. 若点P（a，b）在第二象限内，则a，b的取值范围是（　　）
    A、a＜0，b＞0 B、a＞0，b＞0 C、a＞0，b＜0 D、a＜0，b＜0

    查看试题解析

  • 3. 函数 y=3−x 中自变量x的取值范围是（ ）
    A、x<3 B、x≤3 C、x>3 D、x≥3

    查看试题解析

  • 4. 将一个n边形变成(n＋1)边形，内角和将(　　)
    A、减少180° B、增加90° C、增加180° D、增加360°

    查看试题解析

  • 5. 设正比例函数y=mx的图象经过点A（m，4），且y的值随x的增大而增大，则m=（　　）
    A、2 B、-2 C、4 D、-4

    查看试题解析

  • 6. 一次函数y＝kx－（2－b）的图像如图所示，则k和b的取值范围是（    ）

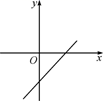    A、k>0，b>2 B、k>0，b<2 C、k<0，b>2 D、k<0，b<2

    查看试题解析

  • 7. 在数学活动课上，老师让同学们判定一个四边形门框是否为矩形，下面是某合作小组的四位同学的拟订方案，其中正确的是（   ）
    A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组对角是否为直角 D、测量两组对边是否相等，再测量对角线是否相等

    查看试题解析

  • 8. 向最大容量为60升的热水器内注水，每分钟注水10升，注水2分钟后停止1分钟，然后继续注水，直至注满.则能反映注水量与注水时间函数关系的图象是 （    ）
    A、 B、 C、 D、

    查看试题解析

  • 9. 如图，已知菱形ABCD的周长是24米，∠BAC＝30°，则对角线BD的长等于（   ）

    A、6 3 米 B、3 3 米 C、6米 D、3米

    查看试题解析

  • 10. 如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E，若AB=8，AD=3，则图中阴影部分的周长为（   ）

    A、16 B、19 C、22 D、25

    查看试题解析

  • 11. 如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OB的方向平移至△O′B′A′的位置，此时点B′的横坐标为5，则点A′的坐标为（　　）

    A、.. B、(2 ， 3) C、(3 ， 3) D、(4 ， 3)

    查看试题解析

  • 12. 在平面直角坐标系中，一矩形上各点的纵坐标不变，横坐标变为原来的 12 ，则该矩形发生的变化为（　　）
    A、向左平移了 12 个单位长度 B、向下平移了 12 个单位长度 C、横向压缩为原来的一半 D、纵向压缩为原来的一半

    查看试题解析

  • 13. 某商店在节日期间开展优惠促销活动：购买原价超过500元的商品，超过500元的部分可以享受打折优惠．若购买商品的实际付款金额y(单位：元)与商品原价x(单位：元)的函数关系的图像如图所示，则超过500元的部分可以享受的优惠是（ ）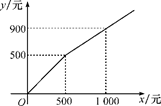

    A、打六折 B、打七折 C、打八折 D、打九折

    查看试题解析

  • 14. 小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中不正确的是（   ）

    A、①② B、②③ C、①③ D、②④

    查看试题解析

二、填空题

  • 15. 当m＝时，函数y＝－（m－2） xm2－3 ＋（m－4）是关于x的一次函数．

    查看试题解析

  • 16. 如图，在△ABC中，AB＝5，BC＝7，EF是△ABC的中位线，则EF的长度范围是 ．

    查看试题解析

  • 17. 一次函数y＝k（x－1）的图象经过点M（－1，－2），则其图象与y轴的交点是 ．

    查看试题解析

  • 18.

    如图，在平面直角坐标系中，△ABC的顶点都在方格纸的格点上，如果将△ABC先向右平移4个单位长度，再向下平移1个单位长度，得到△A1B1C1 ， 那么点A的对应点A1的坐标为 ．

    查看试题解析

  • 19. 如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为10和6时，则阴影部分的面积为 ．

    查看试题解析

  • 20. 如图，已知菱形OABC的顶点O（0，0），B（2，2），则菱形的对角线交点D的坐标为；若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，点D的坐标为 ．

    查看试题解析

三、解答题

  • 21. 如图，左右两幅图案关于y轴对称，右图案中的左右眼睛的坐标分别是（2，3），（4，3），嘴角左右端点的坐标分别是（2，1），（4，1）．

    (1)、试确定左图案中的左右眼睛和嘴角左右端点的坐标；
    (2)、从对称的角度来考虑，说一说你是怎样得到的；
    (3)、直接写出右图案中的嘴角左右端点关于原点的对称点的坐标.

    查看试题解析

  • 22. 为了了解江城中学学生的身高情况，随机对该校男生、女生的身高进行抽样调查．已知抽取的样本中，男生、女生的人数相同，根据所得数据绘制成如图所示的统计图表．

    组别

    身高（cm）

    A

    x<150

    B

    150≤x＜155

    C

    155≤x＜160

    D

    160≤x＜165

    E

    x≥165

    根据图表中提供的信息，回答下列问题：

    (1)、在样本中，男生身高的中位数落在组（填组别序号），女生身高在B组的人数有人；
    (2)、在样本中，身高在150≤x＜155之间的人数共有人，身高人数最多的在组（填组别序号）；
    (3)、已知该校共有男生500人、女生480人，请估计身高在155≤x＜165之间的学生有多少人

    查看试题解析

  • 23. 已知y是x的一次函数，当x＝1时，y＝1；当x＝－2时，y＝－14.

    (1)、求这个一次函数的关系式；
    (2)、在如图所示的平面直角坐标系中作出函数的图象；
    (3)、由图像观察，当0≤x≤2时，函数y的取值范围．

    查看试题解析

  • 24. 顺次连接四边形各边中点所得的四边形叫中点四边形．回答下列问题：
    (1)、只要原四边形的两条对角线 ， 就能使中点四边形是菱形；
    (2)、只要原四边形的两条对角线 ， 就能使中点四边形是矩形；
    (3)、请你设计一个中点四边形为正方形，但原四边形又不是正方形的四边形，把它画出来．

    查看试题解析

  • 25. 王华同学要证明命题“对角线相等的平行四边形是矩形”是正确的，她先作出了如图所示的平行四边形ABCD，并写出了如下不完整的已知和求证．
    (1)、已知：如图1，在平行四边形ABCD中， ，求证：平行四边形ABCD是 ．

    在方框中填空，以补全已知和求证；

    (2)、按王晓的想法写出证明过程；

    证明：

    查看试题解析

  • 26. 如图，直线y1＝2x－2的图像与y轴交于点A，直线y2＝－2x＋6的图像与y轴交于点B，两者相交于点C．

    (1)、方程组 {2x−y=22x+y=6 的解是；
    (2)、当y1＞0与y2＞0同时成立时，x的取值范围为；
    (3)、求△ABC的面积；
    (4)、在直线y1＝2x－2的图像上存在异于点C的另一点P，使得△ABC与△ABP的面积相等，请求出点P的坐标．

    查看试题解析