河北省邯郸市大名县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-05-28 类型：期末考试

进入出卷网下载

一、单选题

1. 要反映台州市某一周每天的最高气温的变化趋势，宜采用( )

A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布统计图

查看试题解析
2. 直角坐标系中，A、B两点的横坐标相同但均不为零，则直线AB（　　）

A、平行于x轴 B、平行于y轴 C、经过原点 D、以上都不对

查看试题解析
3. 函数y＝ $\frac{\sqrt{x}}{x - 2}$ 的自变量x的取值范围是（　　）

A、x≥0且x≠2 B、x≥0 C、x≠2 D、x>2

查看试题解析
4. 已知一次函数 $y = (k - 1) x + 2$ ，若 $y$ 随 $x$ 的增大而增大，则 $k$ 的取值范围是（）

A、 $k > 1$ B、 $k < 1$ C、 $k < 0$ D、 $k > 0$

查看试题解析
5. 某平行四边形的对角线长为x，y，一边长为6，则x与y的值可能是（）

A、4和7 B、5和7 C、5和8 D、4和17

查看试题解析
6. 一个正多边形的内角和是1440°，则它的每个外角的度数是（　　）

A、30° B、36° C、45° D、60°

查看试题解析
7. 如图，在△ABC中，∠ACB=90°，AC=8，AB=10，DE垂直平分AC交AB于点E，则DE的长为（　　）

A、3 B、4 C、5 D、6

查看试题解析
8. 如图，已知函数y＝x+1和y＝ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组 ${\begin{matrix} x - y = - 1 \\ a x - y = - 3 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = - 2 \end{matrix}$ D、 ${\begin{matrix} x = - 2 \\ y = 1 \end{matrix}$

查看试题解析
9. 如图，把一张长方形纸条ABCD沿EF折叠，使点C的对应点C′恰好与点A重合，若∠1＝70°，则∠FEA的度数为（　　）

A、40° B、50° C、60° D、70°

查看试题解析
10. 若直线 $y = k x + 2$ 经过第一、二、四象限，则化简 $| k - 2 |$ 的结果是（）

A、2 + k B、2 - k C、k - 2 D、不能确定

查看试题解析
11. 如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB，BC边上的中点，则MP+PN的最小值是（）

A、 $\frac{1}{2}$ B、1 C、 $\sqrt{2}$ D、2

查看试题解析
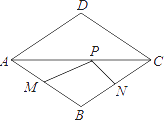12. 如图，在同一直角坐标系中，函数 $y_{1} = 3 x$ 和 $y_{2} = - 2 x + m$ 的图象相交于点A，则不等式 $0 < y_{2} < y_{1}$ 的解集是 $($ $)$

A、 $0 < x < 1$ B、 $0 < x < \frac{5}{2}$ C、 $1 < x < \frac{5}{2}$ D、 $1 < x \leq \frac{5}{2}$

查看试题解析
13. 一个多边形的内角和等于1260°，则从此多边形一个顶点引出的对角线有（）

A、4条 B、5条 C、6条 D、7条

查看试题解析
14. 如图，在正方形ABCD中，点E，F分别在边BC，CD上，且BE＝CF．连接AE，BF，AE与BF交于点G．下列结论不正确的是（　　）

A、AE＝BF B、∠DAE＝∠BFC C、∠AEB+∠BFC＝90° D、AE⊥BF

查看试题解析
15. 如图1，在矩形中，动点从点出发，沿方向运动至点处停止，设点运动的路程为，△BCE的面积为，如果关于的函数图象如图2所示，则当时，点应运动到（　　）

A、点处 B、点处 C、点处 D、点处

查看试题解析
16. 如图，在菱形 $A B C D$ 中， $∠ A = 60 °$ ，点 $E$ 、 $F$ 分别为 $A D$ 、 $D C$ 上的动点， $∠ E B F = 60 °$ ，点 $E$ 从点 $A$ 向点 $D$ 运动的过程中， $A E + C F$ 的长度（　　）

A、逐渐增加 B、逐渐减小 C、保持不变且与 $E F$ 的长度相等 D、保持不变且与 $A B$ 的长度相等

查看试题解析

二、填空题

17. 一个多边形的内角和与外角和的比是4：1，则它的边数是．

查看试题解析
18. 如图，折线ABC是某市在2018年乘出租车所付车费y（元）与行车里程x（km）之间的函数关系图像，观察图像回答，乘客在乘车里程超过3千米时，每多行驶1km，要再付费元．

查看试题解析
19. 如图，在菱形ABCD中，E是AB的中点，且DE⊥AB，AB=10，则∠ABC= ，对角线AC的长为．

查看试题解析

三、解答题

20. 如图，在 $△ ABC$ 中，AD是BC边上的中线，E是AD的中点，延长BE到F，使 $BE = EF$ ，连接AF、CF、DF．

(1)、求证： $AF = BD$ ；

(2)、若 $AB ⊥ AC$ ，试判断四边形ADCF的形状，并证明你的结论．

查看试题解析
21. 如图，直线l经过点A（1，6）和点B（﹣3，﹣2）．

(1)、求直线l的解析式，直线与坐标轴的交点坐标；

(2)、求△AOB的面积．

查看试题解析
22. “大美武汉，畅游江城”．某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校部分学生，要求每位同学选择且只能选择一个最想去的景点，下面是根据调查结果进行数据整理后绘制出的不完整的统计图：

请根据图中提供的信息，解答下列问题：

(1)、求被调查的学生总人数；

(2)、补全条形统计图，并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数；

(3)、若该校共有1200名学生，请估计“最想去景点B“的学生人数．

查看试题解析
23.
如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．

(1)、求证：BM=MN；

(2)、∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．

查看试题解析
24. 如图，直线l：y₁＝﹣ $\frac{5}{4}$ x﹣1与y轴交于点A，一次函数y₂＝ $\frac{3}{4}$ x+3图象与y轴交于点B，与直线l交于点C，

(1)、画出一次函数y₂＝ $\frac{3}{4}$ x+3的图象；

(2)、求点C坐标；

(3)、如果y₁＞y₂ ，那么x的取值范围是．

查看试题解析
25. 如图1，在正方形ABCD中，P是对角线BD上的点，点E在AB上，且PA=PE．

(1)、求证：PC=PE；

(2)、求∠CPE的度数；

(3)、如图2，把正方形ABCD改为菱形ABCD，其他条件不变，试探究∠CPE与∠ABC之间的数量关系，并说明理由．

查看试题解析
26. 某商店经销某种玩具，该玩具每个进价 20 元，为进行促销，商店制定如下“优惠” 方案：如果一次销售数量不超过 5 个，则每个按 50 元销售：如果一次销售数量超过 5 个，则每增加一个，所有玩具均降低 1 元销售，但单价不得低于 30 元，一次销售该玩具的单价 y（元）与销售数量 x（个）之间的函数关系如下图所示．

(1)、结合图形，求出m的值；射线BC所表示的实际意义是什么；

(2)、求线段AB满足的y与x之间的函数解析式，并直接写出自变量的取值范围；

(3)、当销售15个时，商店的利润是多少元．

查看试题解析