河北省邯郸市永年区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-28 类型:期末考试
一、单选题
-
1. 若点A(3,2)与B(-3,m)关于原点对称,则m的值是( )A、3 B、-3 C、2 D、-22. 某校八年级(3)班体训队员的身高(单位:cm)如下:169,165,166,164,169,167,166,169,166,165,获得这组数据方法是( )A、直接观察 B、查阅文献资料 C、互联网查询 D、测量3. 如图,若DE是△ABC的中位线,△ADE的周长为1,则△ABC的周长为( )
 A、1 B、2 C、3 D、44. 若点P(-2,a)在第二象限,则a的值可以是( )A、1 B、-1 C、0 D、-25. 在矩形ABCD中,AB=3,BC=4,E是BC上一点,且与B、C不重合,若AE是整数,则AE等于( )
A、1 B、2 C、3 D、44. 若点P(-2,a)在第二象限,则a的值可以是( )A、1 B、-1 C、0 D、-25. 在矩形ABCD中,AB=3,BC=4,E是BC上一点,且与B、C不重合,若AE是整数,则AE等于( ) A、3 B、4 C、5 D、66. 已知点P到x轴的距离为1,到y轴的距离为2,则点P的坐标不可能为( )A、(1,2) B、(-2,-1) C、(2,-1) D、(2,1)7. 在四边形 中, ,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )A、 B、 C、 D、8. 下列调查中,适宜采用抽样调查方式的是( )A、调查八年级某班学生的视力情况 B、调查乘坐飞机的旅客是否携带违禁物品 C、调查某品牌LED灯的使用寿命 D、学校在给学生订制校服前尺寸大小的调查9. 将某个图形的各个顶点的横坐标都减去2,纵坐标保持不变,可将该图形( )A、向左平移2个单位 B、向右平移2个单位 C、向上平移2个单位 D、向下平移2个单位10. 已知函数y=2x+k-1的图象经过第一、三、四象限,则k的值可以是( )A、3 B、2 C、1 D、011. 在平行四边形ABCD中,数据如图,则∠D的度数为( )
A、3 B、4 C、5 D、66. 已知点P到x轴的距离为1,到y轴的距离为2,则点P的坐标不可能为( )A、(1,2) B、(-2,-1) C、(2,-1) D、(2,1)7. 在四边形 中, ,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )A、 B、 C、 D、8. 下列调查中,适宜采用抽样调查方式的是( )A、调查八年级某班学生的视力情况 B、调查乘坐飞机的旅客是否携带违禁物品 C、调查某品牌LED灯的使用寿命 D、学校在给学生订制校服前尺寸大小的调查9. 将某个图形的各个顶点的横坐标都减去2,纵坐标保持不变,可将该图形( )A、向左平移2个单位 B、向右平移2个单位 C、向上平移2个单位 D、向下平移2个单位10. 已知函数y=2x+k-1的图象经过第一、三、四象限,则k的值可以是( )A、3 B、2 C、1 D、011. 在平行四边形ABCD中,数据如图,则∠D的度数为( ) A、20° B、80° C、100° D、120°12. 如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组 的解是( )
A、20° B、80° C、100° D、120°12. 如图,一次函数y=kx+b与y=x+2的图象相交于点P(m,4),则关于x,y的二元一次方程组 的解是( ) A、 B、 C、 D、13. 某班五个课外小组的人数分布如图所示,若绘制成扇形统计图,则第二小组在扇形统计图中对应的圆心角度数是( )
A、 B、 C、 D、13. 某班五个课外小组的人数分布如图所示,若绘制成扇形统计图,则第二小组在扇形统计图中对应的圆心角度数是( ) A、45° B、60° C、72° D、120°14. 定义运算*为:a*b= 如:1*(-2)=-1×(-2)=2,则函数y=2*x的图象大致是( )A、
A、45° B、60° C、72° D、120°14. 定义运算*为:a*b= 如:1*(-2)=-1×(-2)=2,则函数y=2*x的图象大致是( )A、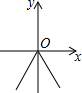 B、
B、 C、
C、 D、
D、
二、填空题
-
15. 函数y= 中,自变量x的取值范围是 .16. 如图,△ABC的顶点都在正方形网格格点上,点A的坐标为(-1,4).将△ABC沿y轴翻折到第一象限,则点C的对应点C′的坐标是 .
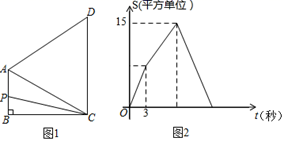
 17. 如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度匀速运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,写出
17. 如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度匀速运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,写出①AB=;
②CD=(提示:过A作CD的垂线);
③BC= .
三、解答题
-
18. 如图是某港口在某天从0时到12时的水位情况变化曲线.
 (1)、在这一问题中,自变量是什么?(2)、大约在什么时间水位最深,最深是多少?(3)、大约在什么时间段水位是随着时间推移不断上涨的?19. 在一次夏令营活动中,主办方告诉营员们A、B两点的位置及坐标分别为(-3,1)、(-2,-3),同时只告诉营员们活动中心C的坐标为(3,2)(单位:km)
(1)、在这一问题中,自变量是什么?(2)、大约在什么时间水位最深,最深是多少?(3)、大约在什么时间段水位是随着时间推移不断上涨的?19. 在一次夏令营活动中,主办方告诉营员们A、B两点的位置及坐标分别为(-3,1)、(-2,-3),同时只告诉营员们活动中心C的坐标为(3,2)(单位:km) (1)、请在图中建立直角坐标系并确定点C的位置;(2)、若营员们打算从点B处直接赶往C处,请用方向角B和距离描述点C相对于点B的位置.20. 某区对即将参加中考的初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
(1)、请在图中建立直角坐标系并确定点C的位置;(2)、若营员们打算从点B处直接赶往C处,请用方向角B和距离描述点C相对于点B的位置.20. 某区对即将参加中考的初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:视力
频数(人)
频率
4.0≤x<4.3
20
0.1
4.3≤x<4.6
40
0.2
4.6≤x<4.9
70
0.35
4.9≤x<5.2
a
0.3
5.2≤x<5.5
10
b
 (1)、本次调查的样本为 , 样本容量为;(2)、在频数分布表中,组距为 , a= , b= , 并将频数分布直方图补充完整;(3)、若视力在4.6以上(含4.6)均属正常,计算抽样中视力正常的百分比.21. 如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件: 画出图形,把截去的部分打上阴影
(1)、本次调查的样本为 , 样本容量为;(2)、在频数分布表中,组距为 , a= , b= , 并将频数分布直方图补充完整;(3)、若视力在4.6以上(含4.6)均属正常,计算抽样中视力正常的百分比.21. 如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件: 画出图形,把截去的部分打上阴影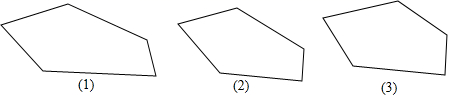 (1)、①新多边形内角和比原多边形的内角和增加了 .
(1)、①新多边形内角和比原多边形的内角和增加了 .②新多边形的内角和与原多边形的内角和相等.
③新多边形的内角和比原多边形的内角和减少了 .
(2)、将多边形只截去一个角,截后形成的多边形的内角和为 ,求原多边形的边数.22. 如图,已知点A,B,C,D的坐标分别为(-2,2),(-2,1),(3,1),(3,2),线段AD、AB、BC组成的图形记作G,点P沿D-A-B-C移动,设点P移动的距离为a,直线l:y=-x+b过点P,且在点P移动过程中,直线l随点P移动而移动,若直线l过点C,求 (1)、直线l的解析式;(2)、求a的值.23. 如图,矩形ABCD中,点E,F分别在边AB,CD上,点G,H在对角线AC上,EF与AC相交于点O,AG=CH,BE=DF.
(1)、直线l的解析式;(2)、求a的值.23. 如图,矩形ABCD中,点E,F分别在边AB,CD上,点G,H在对角线AC上,EF与AC相交于点O,AG=CH,BE=DF. (1)、求证:四边形EGFH是平行四边形;(2)、当EG=EH时,连接AF
(1)、求证:四边形EGFH是平行四边形;(2)、当EG=EH时,连接AF①求证:AF=FC;
②若DC=8,AD=4,求AE的长.
24. 快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:型号
甲
乙
每台每小时分拣快递件数(件)
1000
800
每台价格(万元)
5
3
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)、设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;(2)、购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?