河北省唐山市滦南县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-28 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 ${\begin{array}{l} x = 2, \\ y = - 1 \end{array}$ 是方程 $2 x - a y = 6$ 的一个解，那么 $a$ 的值是（）

A、-2 B、2 C、-4 D、4

查看试题解析
2.
如图，∠1的内错角是（　　）

A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
3. 港珠澳大桥2018年10月24日正式通车，整个大桥造价超过720亿元人民币，720亿用科学记数法表示为（）

A、72×10⁹ B、7.2×10⁹ C、7.2×10¹⁰ D、0.72×10¹¹

查看试题解析
4. 下列等式从左到右的变形，属于因式分解的是（　　）

A、 $x^{2} + 2 x - 1 = {(x - 1)}^{2}$ B、 $(a + b) (a - b) = a^{2} - b^{2}$ C、 $x^{2} + 4 x + 4 = {(x + 2)}^{2}$ D、 $a x^{2} - a = a (x^{2} - 1)$

查看试题解析
5. 如图，将一块三角尺的直角顶点放在直尺的一边上，当 $∠ 1 = 55^{°}$ 时， $∠ 2$ 的度数为（）

A、 $25^{°}$ B、 $35^{°}$ C、 $45^{°}$ D、 $55^{°}$

查看试题解析
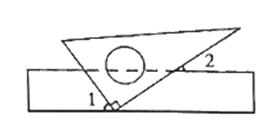6. 不等式组 ${\begin{array}{l} 2 x > - 4 \\ x - 1 \leq 1 \end{array}$ 的解集，在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析
7. 下列各式中，能用完全平方公式因式分解的是（）

A、 $y^{2} - x^{2} + 2 x y$ B、 $x^{2} + y^{2} + x y$ C、 $25 y^{2} + 15 y + 9$ D、 $4 x^{2} + 9 - 12 x$

查看试题解析
8. 下列长度的四根木棒，能与长度分别为2cm和5cm的木棒构成三角形的是（）

A、3 B、4 C、7 D、10

查看试题解析
9. 《九章算术》是中国传统数学名著，其中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问牛、羊各直金几何？”译文：“假设有5头牛，2只羊，值金10两；2头牛，5只羊，值金8两．问每头牛、每只羊各值金多少两？”若设每头牛、每只羊分别值金x两、y两，则可列方程组为（）

A、 ${\begin{matrix} 5 x + 2 y = 10 \\ 2 x + 5 y = 8 \end{matrix}$ B、 ${\begin{matrix} 5 x - 2 y = 10 \\ 2 x - 5 y = 8 \end{matrix}$ C、 ${\begin{matrix} 5 x + 2 y = 10 \\ 2 x - 5 y = 8 \end{matrix}$ D、 ${\begin{matrix} 5 x + 2 y = 8 \\ 2 x + 5 y = 10 \end{matrix}$

查看试题解析
10. 如图，在△ABC中，CD是∠ACB的外角平分线，且CD∥AB，若∠ACB＝100°，则∠B的度数为（　　）

A、35° B、40^o C、45^o D、50^o

查看试题解析
11. 下列计算结果正确的是（）

A、 $a^{2} \cdot a = a^{2}$ B、 $2 a^{2} + a^{2} = 2 a^{2}$ C、 ${(a^{2} b)}^{2} = a^{4} b^{2}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
12. 三条高的交点一定在三角形内部的是（）

A、任意三角形 B、锐角三角形 C、直角三角形 D、纯角三角形

查看试题解析
13. 已知 $2 a + 3 x = 6$ ，要使 $x$ 是负数，则 $a$ 的取值范围是（）

A、 $a > 3$ B、 $a < 3$ C、 $a < - 3$ D、 $- 3 < a < 3$

查看试题解析
14. 如图，三角形ABC 经过平移后得到三角形 DEF，下列说法：①AB∥DE；②AD＝BE；③∠ACB＝∠DFE；④BC＝DE.其中正确的有（）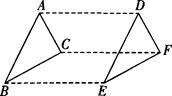

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析
15. 东东是一位密码编译爱好者，在他的密码手册中，有这样一条信息：x-y，a-b，2， $x^{2} - y^{2}$ ，a，x+y分别对应下列六个字：源，丽，美，我，游，渭.现将 $2 a (x^{2} - y^{2}) - 2 b (x^{2} - y^{2})$ 因式分解，结果呈现的密码信息可能是（）

A、我爱美 B、我游渭源 C、美丽渭源 D、美我渭源

查看试题解析
16. 如图，在△ABC中，已知点D、E、F分别是BC、AD、CE的中点，且△ABC的面积为16，则△BEF的面积是（　　）

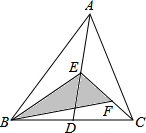A、2 B、4 C、6 D、8

查看试题解析

二、填空题

17. 关于x、y的二元一次方程组 ${\begin{matrix} x + y = 3 \\ 2 x - a y = 5 \end{matrix}$ 的解是 ${\begin{matrix} x = b \\ y = 1 \end{matrix}$ ，则 $a^{b}$ 的值为．

查看试题解析
18. 如果将一副三角板按如图方式叠放，那么∠1 的大小为（度）．

查看试题解析
19. 不等式组 ${\begin{array}{l} x - 3 (x - 1) \leq 7 \\ 2 x + 1 > 3 x \end{array}$ 的整数解为．

查看试题解析
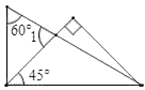20. 若a+b＝4，a﹣b＝1，则（a+2）²﹣（b﹣2）²的值为．

查看试题解析

三、解答题

21. 已知，关于 $x, y$ 的二元一次方程组 ${\begin{matrix} 2 x - 3 y = 7 a - 9 \\ x + 2 y = - 1 \end{matrix}$ 的解满足方程 $2 x - y = 8$ ，求 $a$ 的值.

查看试题解析
22. 某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了不正确，解答过程如下：
原式＝a²+2ab﹣（a²﹣b²）（第一步）

＝a²+2ab﹣a²﹣b²（第二步）

＝2ab﹣b² （第三步）

(1)、该同学解答过程从第步开始出错，不正确原因是；

(2)、写出此题正确的解答过程．

查看试题解析
23. 如图，AB∥CD，△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，GE平分∠FGD.若∠EFG=90°，∠E=35°，求∠EFB的度数.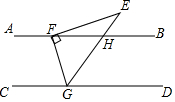

查看试题解析
24. 青年志愿者爱心小分队赴山村送温暖，准备为困难村民购买一些米面.已知购买1袋大米、4袋面粉，共需240元；购买2袋大米、1袋面粉，共需165元.

(1)、求每袋大米和面粉各多少元？

(2)、如果爱心小分队计划购买这些米面共40袋，总费用不超过2140元，那么至少购买多少袋面粉?

查看试题解析
25. 下面是某同学对多项式（x²﹣4x+2）（x²﹣4x+6）+4进行因式分解的过程
解：设x²﹣4x＝y，

原式＝（y+2）（y+6）+4　（第一步）

＝y²+8y+16　（第二步）

＝（y+4）²（第三步）

＝（x²﹣4x+4）²（第四步）

(1)、该同学第二步到第三步运用了因式分解的（填序号）．

A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式

(2)、该同学在第四步将y用所设中的x的代数式代换，得到因式分解的最后结果．这个结果是否分解到最后？．（填“是”或“否”）如果否，直接写出最后的结果．

(3)、请你模仿以上方法尝试对多项式（x²﹣2x）（x²﹣2x+2）+1进行因式分解．

查看试题解析
26. 阅读理解：请你参与下面探究过程，完成所提出的问题.

(1)、问题引入：
如图①，在 $Δ A B C$ 中，点 $O$ 是 $∠ A B C$ 和 $∠ A C B$ 平分线的交点，若 $∠ A = 70^{°}$ ，则 $∠ B O C =$ 度；若 $∠ A = α$ ，则 $∠ B O C =$ （用含 $α$ 的代数式表示）；

(2)、类比探究：
如图②，在 $Δ A B C$ 中， $∠ C B O = \frac{1}{3} ∠ A B C$ ， $∠ B C O = \frac{1}{3} ∠ A C B$ ， $∠ A = α$ .试探究： $∠ B O C$ 与 $∠ A$ 的数量关系（用含 $α$ 的代数式表示），并说明理由.

(3)、知识拓展：
如图③， $B O$ 、 $C O$ 分别是 $Δ A B C$ 的外角 $∠ D B C$ ， $∠ E C B$ 的 $n$ 等分线，它们的交于点 $O$ ， $∠ C B O = \frac{1}{n} ∠ E C B$ ， $∠ B C O = \frac{1}{n} ∠ E C B$ ， $∠ A = α$ ，求 $∠ B O C$ 的度数（用含 $α$ 、 $n$ 的代数式表示）.

查看试题解析