河北省唐山市乐亭县2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-28 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，△ABC中的边BC上的高是（　　）

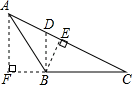A、AF B、DB C、CF D、BE

查看试题解析
2. 如图，数轴所表示的不等式的解集是（）

A、 $x > 1$ B、 $x < 1$ C、 $x \geq 1$ D、 $x \leq 1$

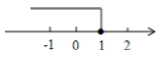查看试题解析
3. 下列计算正确的是（）

A、 $2 a + a^{2} = 3 a^{2}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $3 a^{2} - 2 a = a^{2}$

查看试题解析
4. 已知三角形三边长分别为5、a、9，则数a可能是(　　)

A、4 B、6 C、14 D、15

查看试题解析
5. 已知a＜b，下列变形正确的是（）

A、a﹣3＞b﹣3 B、2a＜2b C、﹣5a＜﹣5b D、﹣2a+1＜﹣2b+1

查看试题解析
6. 下列多项式中能用平方差公式分解因式的是(　　)

A、x²+4 B、x²-xy C、x²-9 D、-x²-y²

查看试题解析
7. △ABC 的内角分别为∠A 、∠B 、∠C ，下列能判定△ABC 是直角三角形的条件是（）

A、∠A = 2∠B = 3∠C B、∠C = 2∠B C、∠A : ∠B :∠C = 3 : 4 : 5 D、∠A + ∠B = ∠C

查看试题解析
8. $81^{3} - 81$ 不能被（）整除.

A、80 B、81 C、82 D、83

查看试题解析
9. 若关于x、y的二元一次方程组 ${\begin{array}{l} x + 3 y = 2 + a \\ 3 x + y = - 4 a \end{array}$ 的解满足x＋y＞2，则a的取值范围为（）

A、a＜−2 B、a＞−2 C、a＜2 D、a＞2

查看试题解析
10. 如图，△ABC是一把直角三角尺，∠ACB＝90°，∠B＝30°．把三角尺的直角顶点放在一把直尺的一边上，AC与直尺的另一边交于点D，AB与直尺的两条边分别交于点E，F．若∠AFD＝58°，则∠BCE的度数为（）

A、20° B、28° C、32° D、88°

查看试题解析
11. 已知x²+kx+16可以用完全平方公式进行因式分解，则k的值为(　　)

A、-8 B、±4 C、8 D、±8

查看试题解析
12. 若 $x = - 3$ 是关于 $x$ 的方 $x = m + 1$ 的解，则关于 $y$ 的不等式 $2 (1 - 2 y) \geq - 6 + m$ 的最大整数解为（）

A、1 B、2 C、3 D、4

查看试题解析
13. 如图，△ABC中，∠C=90°，BC=6，AC=8，点E是AB的中点，BD=2CD，则△BDE的面积是（）

A、4 B、6 C、8 D、12

查看试题解析
14. 已知不等式：① $x > 1$ ，② $x > 4$ ，③ $x < 2$ ，④ $2 - x > - 1$ ，从这四个不等式中取两个，构成正整数解是2的不等式组是（）

A、①与② B、②与③ C、③与④ D、①与④

查看试题解析
15. 某种服装的进价为240元，出售时标价为360元，由于换季，商店准备打折销售，但要保特利润不低20%，那么至多打（）

A、6折 B、7折 C、8折 D、9折

查看试题解析
16. 对于实数x，我们规定[x]表示不大于x的最大整数，例如[1.2]=1，[3]=3，[-2.5]=-3，若[1- $\frac{x - 1}{2}$ ]=5，则x的取值范围是(　　)

A、-7＜x≤-5 B、-7≤x＜-5 C、-9≤x＜-7 D、-9＜x≤-7

查看试题解析

二、填空题

17. 数据0.0005用科学记数法表示为．

查看试题解析
18. 如图，∠1的度数为.

查看试题解析
19. 已知关于x的不等式(a-2)x＞1的解集为x＜ $\frac{1}{a - 2}$ ，则a的取值范围.

查看试题解析
20. 如图，在第1个 $Δ A B A_{1}$ 中， $∠ B =$ 40°， $∠ B A A_{1} = ∠ B A_{1} A$ ，在 $A_{1} B$ 上取一点 $C$ ，延长 $A A_{1}$ 到 $A_{2}$ ，使得在第2个 $Δ A_{1} C A_{2}$ 中， $∠ A_{1} C A_{2} = ∠ A_{1} A_{2} C$ ；在 $A_{2} C$ 上取一点 $D$ ，延长 $A_{1} A_{2}$ 到 $A_{3}$ ，使得在第3个 $Δ A_{2} D A_{3}$ 中， $∠ A_{2} D A_{3} = ∠ A_{2} A_{3} D$ ；…，按此做法进行下去，第3个三角形中以 $A_{3}$ 为顶点的内角的度数为；第 $n$ 个三角形中以 $A_{n}$ 为顶点的内角的度数为度.

查看试题解析

三、解答题

21. 若a，b，c是△ABC的三边，且a，b满足关系式|a-6|+(b-8)²=0，c是不等式组 ${\begin{array}{l} \frac{2 x + 5}{4} > x - 4 \\ 3 (x + 2) < 4 x + 1 \end{array}$ 的最大整数解，求△ABC的周长．

查看试题解析
22. 如图，一长方形模具长为2a，宽为a，中间开出两个边长为b的正方形孔．

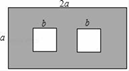(1)、求图中阴影部分面积（用含a、b的式子表示）

(2)、用分解因式计算当a＝15.7，b＝4.3时，阴影部分的面积．

查看试题解析
23. 如图，D、E、F分别在△ABC的三条边上，DE∥AB，∠1+∠2=180°.

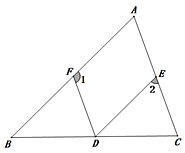(1)、试说明：DF∥AC；

(2)、若∠1=110°，DF平分∠BDE，求∠C的度数.

查看试题解析
24. 观察下列各式：① $4 \times 1 \times 2 + 1 = {(1 + 2)}^{2}$ ；② $4 \times 2 \times 3 + 1 = {(2 + 3)}^{2}$ ；③ $4 \times 3 \times 4 + 1 = {(3 + 4)}^{2} \cdot \cdot \cdot$ ．

(1)、根据你观察、归纳、发现的规律，写出 $4 \times 2012 \times 2013 + 1$ 可以是的平方．

(2)、试猜想写出第 $n$ 个等式，并说明成立的理由．

(3)、利用前面的规律，将 $4 (\frac{1}{2} x^{2} + x) (\frac{1}{2} x^{2} + x + 1) + 1$ 改成完全平方的形式为：．

查看试题解析
25. 某大学公益组织计划购买 $A 、 B$ 两种的文具套装进行捐赠，关注留守儿童经洽谈，购买 $A$ 套装比购买 $B$ 套装多用20元，且购买5套 $A$ 套装和4套 $B$ 套装共需820元．

(1)、求购买一套 $A$ 套装文具、一套 $B$ 套装各需要多少元？

(2)、根据该公益组织的募捐情况和捐助对象情况，需购买 $A 、 B$ 两种套装共60套，要求购买 $A 、 B$ 两种套装的总费用不超过5240元，则购买 $A$ 套装最多多少套？

查看试题解析
26. 探究与发现：
如图1所示的图形，像我们常见的学习用品--圆规．我们不妨把这种图形叫做“规形图”，那么在这一个简单的图形中，到底隐藏了哪些数学知识呢？请解决以下问题：

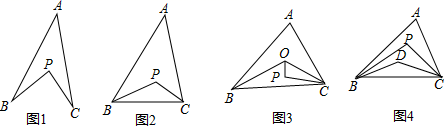(1)、观察“规形图”，试探究∠BPC与∠A、∠B、∠C之间的关系，并说明理由；

(2)、请你直接利用以上结论，解决以下问题：
①如图2：已知△ABC，BP平分∠ABC，CP平分∠ACB，直接写出∠BPC与∠A之间存在的等量关系为：．

迁移运用：如图3：在△ABC中，∠A=80°，点O是∠ABC，∠ACB角平分线的交点，点P是∠BOC，∠OCB角平分线的交点，若∠OPC=100°，则∠ACB的度数．

②如图4：若D点是△ABC内任意一点，BP平分∠ABD，CP平分∠ACD．直接写出∠BDC、∠BPC、∠A之间存在的等量关系为．

查看试题解析