河北省石家庄市长安区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-28 类型：期末考试

进入出卷网下载

一、单选题

1. 把58000表示成a×10ⁿ(其中1≤a≤10，n为整数)的形式，则n=(　　)

A、-4 B、2 C、3 D、4

查看试题解析
2. 如图，∠3的同位角是（）

A、∠1 B、∠2 C、∠B D、∠C

查看试题解析
3. 下列等式从左到右的变形是因式分解的是（）

A、 $12 a^{2} b = 3 a \cdot 4 a b$ B、 $(x + 3) (x - 3) = x^{2} - 9$ C、 $a x - a y = a (x - y)$ D、 $4 x^{2} + 8 x - 1 = 4 x (x + 2) - 1$

查看试题解析
4. 如图，已知直线AB与CD平行，直线EF与AB，CD分别交于点E，F，若∠1=125°，则∠2=(　　)

A、65° B、55° C、50° D、45°

查看试题解析
5. 下列各式中，计算结果为a⁸的是(　　)

A、 $a^{4} + a^{4}$ B、 $a^{16} \div a^{2}$ C、 $a^{4} \cdot a^{4}$ D、 ${(- 2 a^{4})}^{2}$

查看试题解析
6. 若一个三角形两边长分别是5cm和8cm，则第三边长可能是(　　)

A、14cm B、13cm C、10cm D、-3cm

查看试题解析
7. 如图是测量嘉琪跳远成绩的示意图，直线l是起跳线，以下线段的长度能作为嘉琪跳远成绩的是（）

A、BP B、CP C、AP D、AO

查看试题解析
8. 解方程组 ${\begin{array}{l} 3 m + 4 n = 10 ① \\ 4 m - 3 n = 5 ② \end{array}$ ，如果用加减消元法消去n，那么下列方法可行的是(　　)

A、①×4+②×3 B、①×4-②×3 C、①×3-②×4 D、①×3+②×4

查看试题解析
9. 一副三角板如图放置，点D在CB的延长线上，EF∥CD，∠C=∠EDF=90°，∠A=45°，∠EFD=30°，则∠DFB=(　　)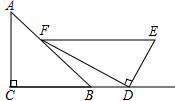

A、15° B、20° C、25° D、30°

查看试题解析
10. 下列命题：①对顶角相等；②内错角相等；③两条平行线之间的距离处处相等；④有且只有一条直线垂直于已知直线．其中是假命题的有(　　)

A、①② B、②④ C、②③ D、③④

查看试题解析
11. 如图，已知有理数a，b，c在数轴上对应的点分别为A，B，C，则下列不等式中不正确的是(　　)

A、c＜b＜a B、ac＞ab C、cb＞ab D、c+b＜a+b

查看试题解析
12. 已知 $x^{2} - 4 x - 1 = 0$ ，则代数式 $2 x (x - 3) - {(x - 1)}^{2} + 3$ 的值为（）

A、 $3$ B、 $2$ C、 $1$ D、 $- 1$

查看试题解析
13. 关于x的不等式 ${\begin{matrix} 2 (x - 1) > 4 \\ a - x < 0 \end{matrix}$ 的解集为x＞3，那么a的取值范围为（）

A、a＞3 B、a＜3 C、a≥3 D、a≤3

查看试题解析
14. 若x﹣m与x+3的乘积中不含x的一次.则m的值为（）

A、3 B、1 C、0 D、﹣3

查看试题解析
15. 在锐角三角形ABC中，∠A=50°，则∠B的范围是(　　)

A、0°＜∠B＜90° B、40°＜∠B＜130° C、40°≤∠B≤90° D、40°＜∠B＜90°

查看试题解析
16. 如图，在长方形ABCD中，AB=5，第一次平移将长方形ABCD沿AB方向向右平移4个单位长度，得到长方形A₁B₁C₁D₁ ，第二次平移将长方形A₁B₁C₁D₁沿A₁B₁方向向右平移4个单位长度，得到长方形A₂B₂C₂D₂ ， ……，第n次平移将长方形A_n-1B_n-1C_n-1D_n-1沿A_n-1B_n-1方向向右平移4个单位长度，得到长方形A_nB_nC_nD_n(n＞2)．若AB_n的长为45，则n=(　　)

A、10 B、11 C、16 D、9

查看试题解析

二、填空题

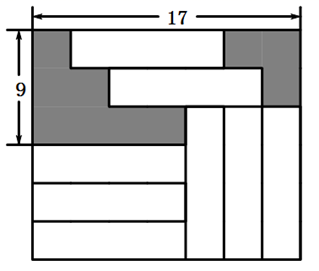
17. 已知关于x，y的二元一次方程mx-2y=2的一组解为 ${\begin{matrix} x = 3 \\ y = 5 \end{matrix}$ ，则m= ．

查看试题解析
18. 若有理数a，b满足|a+ $\frac{1}{2}$ |+b²=0，则a^b= ．

查看试题解析
19. 分解因式：x³y﹣2x²y+xy= ．

查看试题解析
20. 在如图所示的长方形中放置了8个形状、大小都相同的小长方形，则图中阴影部分的面积为．

查看试题解析

三、解答题

21. 计算：

(1)、解方程组： ${\begin{matrix} 2 m - n = 4 \\ 2 m + 3 n = 12 \end{matrix}$ ；

(2)、解不等式组 ${\begin{matrix} 2 (x - 1) \geq 3 x - 7 \\ x - 2 \geq 6 - 3 x \end{matrix}$ ，并把解集在数轴上表示出来．

(3)、(x+1)(x+2)-=6x+2，横线内应填写的式子是．

查看试题解析
22. 在多项式的乘法公式中，完全平方公式是其中重要的一个．

(1)、请你补全完全平方公式的推导过程：
(a+b)²=(a+b)(a+b)=a²+++b²=a²++b²

(2)、如图，将边长为a+b的正方形分割成I，Ⅱ，Ⅲ，Ⅳ四部分，请用不同的方法分别表示出这个正方形的面积，并结合图形给出完全平方公式的几何解释．

查看试题解析
23. 请同学们观察以下三个等式，并结合这些等式，回答下列问题．

(1)、请你再写出另外两个符合上述规律的算式：，；

(2)、观察上述算式，我们发现：如果设两个连续奇数分别为2n-1和2n+1(其中n为正整数)，则它们的平方差是8的倍数．请用含n的式子说明上述规律的符合题意性．

查看试题解析
24. 如图，AD，AE和AF分别是△ABC的高、角平分线和中线．

(1)、对于下面的五个结论：①BC=2BF；②∠CAE= $\frac{1}{2}$ ∠CAB；③BE=CE；④AD⊥BC；⑤S_△_AFB=S_△_ADC ．其中不正确的是(只填序号)；

(2)、若∠C=70°，∠ABC=28°，求∠DAE的度数．

查看试题解析

25. 某超市分别以每盏150元，190元的进价购进A，B两种品牌的护眼灯，下表是近两天的销售情况．

销售日期	销售数量(盏)		销售收入(元)
销售日期	A品牌	B品牌	销售收入(元)
第一天	2	1	680
第二天	3	4	1670

(1)、求A，B两种品牌护眼灯的销售价；

(2)、若超市准备用不超过4900元的金额购进这两种品牌的护眼灯共30盏，求B品牌的护眼灯最多采购多少盏？

查看试题解析

26. [问题解决]：如图1，已知AB∥CD，E是直线AB，CD内部一点，连接BE，DE，若∠ABE=40°，∠CDE=60°，求∠BED的度数．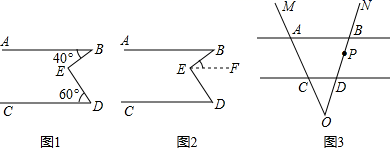

嘉琪想到了如图2所示的方法，但是没有解答完，下面是嘉淇未完成的解答过程：

解：过点E作EF∥AB，

∴∠ABE=∠BEF=40°

∵AB∥CD，

∴EF∥CD，

…

(1)、请你补充完成嘉淇的解答过程：

(2)、当点P在B，D两点之间运动时(P不与B，D重合)，求α，β和∠APC之间满足的数量关系．

(3)、当点P在B，D两点外侧运动时(P不与点O重合)，直接写出α，β和∠APC之间满足的数量关系．

查看试题解析