河北省邯郸市邱县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-05-28 类型:期末考试
一、单选题
-
1. 下列语句:
①不相交的两条直线叫平行线
②在同一平面内,两条直线的位置关系只有两种:相交和平行
③如果线段AB和线段CD不相交,那么直线AB和直线CD平行
④如果两条直线都和第三条直线平行,那么这两条直线平行
⑤过一点有且只有一条直线与已知直线平行
正确的个数是( )
A、1 B、2 C、3 D、42. 王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?( )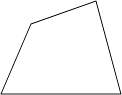 A、0根 B、1根 C、2根 D、3根3. 如图所示,下列结论中不正确的是
A、0根 B、1根 C、2根 D、3根3. 如图所示,下列结论中不正确的是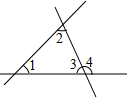 A、 和 是同位角 B、 和 是同旁内角 C、 和 是同位角 D、 和 是内错角4. 下列图形中,线段MN的长度表示点M到直线l的距离的是( )A、
A、 和 是同位角 B、 和 是同旁内角 C、 和 是同位角 D、 和 是内错角4. 下列图形中,线段MN的长度表示点M到直线l的距离的是( )A、 B、
B、 C、
C、 D、
D、 5. 如果单项式 与 是同类.那么关于 的方程 的解为( )A、 B、 C、 D、 .6. 如图,AB∥EF,则α、β、γ的关系是( )
5. 如果单项式 与 是同类.那么关于 的方程 的解为( )A、 B、 C、 D、 .6. 如图,AB∥EF,则α、β、γ的关系是( )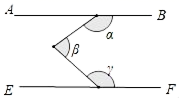 A、β+γ﹣α=90° B、α+β+γ=360° C、α+β﹣γ=90° D、β=α+γ7. 某种牌子的书包,进价为m元,加价n元后作为定位出售,如果元旦期间按定价的八折销售,那么元旦期间的售价为 元.A、 B、 C、 D、8. 若 ,则它们的大小关系是( )A、a<b<c<d B、a<d<c<b C、b<a<d<c D、c<a<d<b9. 如果多项式 是一个完全平方式,则m的值是 ( )A、±4 B、4 C、8 D、± 810. 一款新型的太阳能热水器进价2000元,标价3000元,若商场要求以利润率不低于5%的售价打折出售,则设销售员出售此商品最低可打x折,由题意列方程,得( )A、 B、 C、 D、11. 如图,给出下列条件:①∠3=∠4,②∠1=∠2,③∠D=∠DCE,④∠B=∠DCE,其中能判断AB∥CD的是( )
A、β+γ﹣α=90° B、α+β+γ=360° C、α+β﹣γ=90° D、β=α+γ7. 某种牌子的书包,进价为m元,加价n元后作为定位出售,如果元旦期间按定价的八折销售,那么元旦期间的售价为 元.A、 B、 C、 D、8. 若 ,则它们的大小关系是( )A、a<b<c<d B、a<d<c<b C、b<a<d<c D、c<a<d<b9. 如果多项式 是一个完全平方式,则m的值是 ( )A、±4 B、4 C、8 D、± 810. 一款新型的太阳能热水器进价2000元,标价3000元,若商场要求以利润率不低于5%的售价打折出售,则设销售员出售此商品最低可打x折,由题意列方程,得( )A、 B、 C、 D、11. 如图,给出下列条件:①∠3=∠4,②∠1=∠2,③∠D=∠DCE,④∠B=∠DCE,其中能判断AB∥CD的是( )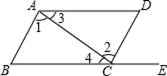 A、①或④ B、②或④ C、②或③ D、①或③12. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( )
A、①或④ B、②或④ C、②或③ D、①或③12. 将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为( ) A、75° B、65° C、60° D、45°13. 如图,两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是也相等,则一块巧克力的质量是( )
A、75° B、65° C、60° D、45°13. 如图,两架天平保持平衡,且每块巧克力的质量相等,每个果冻的质量也相等,则一块巧克力的质量是也相等,则一块巧克力的质量是( ) A、20g B、25g C、15g D、30g14. 一个两位数,十位上的数字比个位上的数字大1,若将个位与十位上的数字对调,得到的新数比原数小9,设个位上的数字为x,十位上的数字为y,根据题意,可列方程为( )A、 B、 C、 D、15. 今年某市有30000名考生参加中考,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )A、每位考生的数学成绩是个体 B、30000名考生是总体 C、这100名考生是总体的一个样本 D、1000名学生是样本容量16. 有长为1cm、2cm、3cm、4cm的四根木棒,选其中的3根作为三角形的边,可以围成的三角形的个数是( )A、1个 B、2个 C、3个 D、4个
A、20g B、25g C、15g D、30g14. 一个两位数,十位上的数字比个位上的数字大1,若将个位与十位上的数字对调,得到的新数比原数小9,设个位上的数字为x,十位上的数字为y,根据题意,可列方程为( )A、 B、 C、 D、15. 今年某市有30000名考生参加中考,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )A、每位考生的数学成绩是个体 B、30000名考生是总体 C、这100名考生是总体的一个样本 D、1000名学生是样本容量16. 有长为1cm、2cm、3cm、4cm的四根木棒,选其中的3根作为三角形的边,可以围成的三角形的个数是( )A、1个 B、2个 C、3个 D、4个二、填空题
-
17. 如图,点O是直线AB上一点,OC⊥OD,OM是∠BOD的角平分线,ON是∠AOC的角平分线,则∠MON的度数是°.
 18. 方程 ,▲处被墨水盖住了,已知方程的解x=2,那么▲处的数字是.19. 若am=16,an=2,则am﹣2n的值为.20. 若 ,则 .
18. 方程 ,▲处被墨水盖住了,已知方程的解x=2,那么▲处的数字是.19. 若am=16,an=2,则am﹣2n的值为.20. 若 ,则 .三、解答题
-
21.(1)、分解因式 .(2)、先化简再求值: ,其中 , .22. 方程mx+ny=1的两个解是 , ,求m和n的值.23. 如图,已知 ,B,E,C,F在同一直线上.
 (1)、若 , ,求 的度数;(2)、若 , ,求BF的长.24. 某中学为了了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图,请根图中提供的信息,解答下列问题:
(1)、若 , ,求 的度数;(2)、若 , ,求BF的长.24. 某中学为了了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图,请根图中提供的信息,解答下列问题: (1)、参加调查的人数共有人;(2)、将条形图补充完整;(3)、求在扇形图中表示“其它球类”的扇形的圆心角的度数.25. 列方程解应用题:为了保护环境,节约用水,按照《关于调整市水务(集团)有限公司自来水价格的通知》规定对供水范围内的居民用水实行三级阶梯水价收费如下表:
(1)、参加调查的人数共有人;(2)、将条形图补充完整;(3)、求在扇形图中表示“其它球类”的扇形的圆心角的度数.25. 列方程解应用题:为了保护环境,节约用水,按照《关于调整市水务(集团)有限公司自来水价格的通知》规定对供水范围内的居民用水实行三级阶梯水价收费如下表:每户每月用水量
水费价格(单位:元/立方米)
不超过22立方米
2.3
超过22立方米且不超过30立方米的部分
a
超过30立方米的部分
4.6
(1)、若小明家去年1月份用水量20立方米,他家应缴费元.(2)、若小明家去年2月份用水量26立方米,缴费64.4元,请求出用水在22-30立方米之间收费标准a元/立方米?(3)、在(2)的条件下,若小明家去年8月份用水量增大,共缴费87.4元,请求出他家8月份的用水量多少立方米?26. 如图,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处. (1)、若∠PEF=48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为.(2)、若∠PEF=75°,∠CFQ= ∠PFC,求∠EFP的度数.
(1)、若∠PEF=48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为.(2)、若∠PEF=75°,∠CFQ= ∠PFC,求∠EFP的度数.