山东省泰安市高新区2020年中考数学一模试卷
试卷更新日期：2020-05-26 类型：中考模拟
一、选择题
-
1. 下列各数中，负数是（ ）A、|-3| B、-（-1） C、 D、2. 下列运算正确的是（ ）A、2x²+x3=3x5 B、（-3x4y²）²=-6x8y4 C、2x2.x³=2x5 D、4x8÷2x²=2x43. 在正面完全相同、反面印有下列四个图形的纸片中，任抽一张，则抽到的图形中，既是轴对称图形，又是中心对称图形的概率是（ ）
A、 B、 C、 D、14. 2020年2月，国家电网整理了各省对总公司“应对疫情12条举措”的响应方案及执行进展。其中，山东基础建设投资金额约220亿元，为我省重大项目和新旧动能转换项目提供坚强电力保障。其中，数据220亿元用科学记数法表示为（ ）A、220×106元 B、22×108元 C、2.2×109元 D、2.2×1010元5. 将一副三角板按如图所示的位置摆放在直尺上，则∠1的度数为（ ）
A、60° B、65° C、75° D、85°6. 我区某中学组织的全校师生迎“五四”诗词大赛中，25名参赛同学的得分情况如图所示。这些同学成绩的中位数和众数分别是（ ）
A、96分，98分 B、97分，98分 C、98分，96分 D、97分，96分7. 如图，在⊙O中，四边形ABCD测得∠ABC=150°，连接AC，若⊙O的半径为4，则AC的长为（ ）。
A、2 B、2 C、4 D、48. 若不等式组 有3个整数解，则a的取值范围是（ ）A、 ≤a<-1 B、 <a≤-1 C、 <a≤3 D、 ≤a<39. 在同一平面直角坐标系中，二次函数y1=ax²+bx与一次函数y2=ax+b的大致图象可能是（ ）A、
B、
C、
D、
10. 泰山风景区推出“5G+智慧泰山”，5G是未来社会的基础设施，是国家战略。5G网络峰值速率是4G网络峰值速率的10倍，在峰值速率下传输1000兆数据，5G网络比4G网络快约90秒，求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输x兆数据，依题意，可列方程是（ ）A、 B、 C、 D、11. 如图是二次函数y=ax²+bx+c的图象，下列结论：
①ac>0，②2a+b>0，③4ac<b²，④a+b+c<0，⑤当x>0时，y随x的增大而减小；其中正确的个数有（ ）
A、1个 B、2个 C、3个 D、4个12. 如图，Ｍ、N是正方形ABCD的边CD上的两个动点，满足AM=BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为2，则线段CF的最小值是（ ）
A、2 B、1 C、 -1 D、 -2二、填空题
-
13. 关于x的一元二次方程ax2+3ax+2=0有两个相等的实数根，则a的取值为。14. 矩形ABCD的两条对称轴为坐标轴，点A的坐标为（2，1），一张透明纸上画有一个点E和一条抛物线，平移透明纸，使点E与点A重合，此时抛物线的函数表达式为y=x²，再次平移透明纸，使点E与点C重合，则该抛物线的函数表达式变为。15. 如图，在⊙O中，AE与⊙O相切于点A，直径DB与AE交于点E，弦BC与AC交于点C，∠CAD=30°，∠E=30°，BC=2，则AC的长为。
16. 如图，一艘轮船在A处测得灯塔P位于其北偏东60°方向上，轮船沿正东方向航行20海里到达B处后，测得灯塔P位于其北偏东30°方向上，轮船沿计划路线航行时与灯塔Ｐ的距离最少是海里。（结果保留根号）
17. 如图，在矩形ABCD中，AB=2，BC=4，点Ｍ、N分别在边AD和BC上，沿MN折叠四边形ABCD，使点A、B分别落在A1、B1处，得四边形A1B1NM，点B1在DC上，过点M作ME⊥BC于点E，连接BB1 ， 则下列结论：①∠MNB1=∠ABB1； ②△ＭEN∽△BCB1；③ ；④若点B1是CD的中点，则AM= ，其中，正确结论的序号是（把所有正确结论的序号都在填在横线上）
18. 如图所示，在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5……过A1、A2、A3、A4、A5……分别作x轴的垂线与反比例函数y= 的图象交于点P1、P2、P3、P4、P5……并设△OA1P1、△A1A2P2、△A2A3P3……面积分别为S1、S2、S3……，按此作法进行下去，则S2020的值为。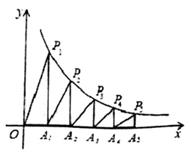
三、解答题
-
19. 先化简，再求值： ，其中m= -20. 4月23日是世界读书日，设立的目的是推动更多的人去阅读和写作.为了解学生的课外阅读情况，对某校八年级1班“你最喜爱的课外阅读书目”进行调查（每名学生必须选一类且只能选一类阅读书目），并根据调查结果绘制成如图所示的两幅统计图（不完整）。
根据以上信息解决下列问题
(1)、所抽查的学生中，选史学类的男生有人，选哲学类的女生有人；(2)、扇形统计图中“科学类”所对应扇形圆心角度数为 °；(3)、若该校有2000名学生，请估计该校喜爱“科学类”的学生共有多少人？(4)、从所抽取的选“哲学类”的学生中，随机选取两名学生参加区级辩论赛，请用树状图或列表法求出所选取的两名学生恰好选中一个男生、一个女生的概率。21. 如图，△OAB在平面直角坐标系中，∠BAO=90°，将△OAB绕点O顺时针旋转，使点B落在点D处，得到△ODE，过点B作平行于x轴的直线交OE于点F，交y轴于点N，直线FM交OB于点M。S△OAB=16，tan∠DOE= 。
(1)、求经过点M、F的反比例函数）y1= 和直线FM：y2=k2x+b的解析式；(2)、过点Ｍ作MH⊥x轴，求五边形NFMHO的面积；(3)、直接写出当 >k2x+b时x的值。22. 如图1，∠DAB是平行四边形ABCD的内角，∠DAB=60°。
(1)、若BF平分∠ABC，交AD于点F，过点A作AG∥BF，过点F作FG∥AB。判断四边形ABFG的形状：；
(2)、旋转∠DAB到∠FAE，如图2，边AF交BC于点E，在边AF上截取AF=AE，连接EF，问：BF是否平分∠ABC，若是请证明，若不是，请说明理由；(3)、在（2）的条件下，过点A作AGE F，过点F作FGAE，若恰好EGAB，如图3，连接DG并延长，交BA的延长线于点H，求证：BC=3AB。23. 科技改变世界，随着科技的发展，自动化程度越来越高，机器人市场越来越火，某商场购进一批A，B两种品牌的编程机器人，进价分别为每台3000元、4000元，市场调查发现：销售3个A品牌机器人和2个B品牌机器人，可获利润6000元；销售2个A品牌机器人和3个B品牌机器人，可获利润6500元。(1)、此商场A，B两种品牌的编程机器人销售价格分别是多少元？(2)、若商场准备用不多于65000元的资金购进A，B两种品牌的编程机器人共20个，则至少需要购进A品牌的编程机器人多少个？(3)、不考虑其它因素，商场打算B品牌编程机器人数量不多于A品牌编程机器人数量的 ，现打算购进A，B两种品牌编程机器人共40个，怎样进货才能获得最大的利润？24. 如图，等腰直角△ABC中，AB=4，∠BAC=90°，P是BC上一点，过P作PE⊥AP，过点C作CE∥AB交PE于点E，连接AE，将△PCE沿PC翻折得到△PCF，延长FP交AB于H，PE交AC于G。
(1)、若BP=3PC，求AE的长；(2)、若AP²=AH·AB，求CG的长。25. 如图，抛物线y=ax²+bx+c（a≠0）交直线AC： y= x-4于点A，点C两点，且过点B（4，0），连接AC，BC。
(1)、求此抛物线的表达式与顶点坐标；(2)、点Ｐ是第四象限内抛物线上的一个动点，过点P作PM⊥x轴，垂足为点Ｍ，PM交BC于点Q。设点P的横坐标为m，试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形。若存在，请求出此时点Ｑ的坐标，若不存在，请说明理由；(3)、若点E在x轴上，点F在抛物线上，是否存在以点B，C，E，F为顶点的平行四边形？若存在，求点F的坐标；若不存在，请说明理由。