河北省2020年中考数学二模试卷

试卷更新日期：2020-05-26 类型：中考模拟

进入出卷网下载

一、选择题

1. 使分式 $\frac{x}{2 x - 4}$ 有意义的x的取值范围是（）

A、x=2 B、x≠2 C、x=-2 D、x≠0

查看试题解析
2. 下列手机手势解锁图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 国家发改委2月7日紧急下达第二批中央预算内投资2亿元人民币，专项补助承担重症感染患者救治任务的湖北多家医院重症治疗病区建设，其中数据2亿用科学记数法表示为（）

A、2×10⁷ B、2×10⁸ C、20×10⁷ D、0.2×10⁸

查看试题解析
4. 如图，在线段AB上有C，D两点，CD长度为 $1 c m$ ，AB长为整数，则以A，B，C，D为端点的所有线段长度和不可能为（）

A、 $21 c m$ B、 $22 c m$ C、 $25 c m$ D、 $31 c m$

查看试题解析
5. 如图所示，已知直线AB，CD相交于O，OE平分∠COB，若∠EOB=55°，则∠BOD的度数是（）

A、20° B、25° C、30° D、70°

查看试题解析
6. 甲、乙、丙、丁四位同学在一次数学测验中的平均成绩是90分，而甲、乙、丙三人的平均成绩是88分，下列说法一定正确的是（　　）

A、丁同学的成绩比其他三个同学的成绩都好 B、四位同学成绩的中位数一定是其中一位同学的成绩 C、四位同学成绩的众数一定是90分 D、丁同学成绩是96分

查看试题解析
7. 如右图，在一幅矩形风景画外面的四周镶一条金色纸边，制成一幅矩形挂图，整个挂图的长80cm，宽50cm如图所示，如果风景画的面积是3500cm²，设金色纸边的宽为xcm，那么x满足的方程是（）

A、（80-x）（50-x）=3500 B、（80-2x）（50-2x）=3500 C、（80+x）（50+x）=3500 D、（80+2x）（50+2x）-3500

查看试题解析
8. 已知，如图在直角坐标系中，点A在y轴上，BC⊥x轴于点C，点A关于直线OB的对称点D恰好在BC上，点E与点O关于直线BC对称，∠OBC=35°，则∠OED的度数为（　　）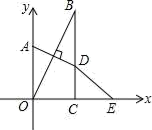

A、10° B、20° C、30° D、35°

查看试题解析
9. 如图，在Rt△ABC中， $∠ A C B = 90 °$ ， $\frac{B C}{A C} = \frac{3}{4}$ ，过点 $C$ 作 $C D ⊥ A B$ ，垂足为 $D$ ，则 $\frac{B D}{A D}$ 的值为（）

A、 $\frac{3}{4}$ B、 $\frac{9}{16}$ C、 $\frac{16}{9}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
10. 当-2≤x≤1时，二次函数y=-（x-m）²+m²+1有最大值4，则实数m的值为（）

A、 $- \frac{7}{4}$ B、 $\sqrt{3}$ 或- $\sqrt{3}$ C、2或- $\sqrt{3}$ D、2或- $\sqrt{3}$ 或 $- \frac{7}{4}$

查看试题解析
11. 如图，直角坐标系中，A是反比例函数y= $\frac{12}{x}$ （x>0）图象上一点，B是y轴正半轴上一点，以OA，AB为邻边作 $▱$ ABCO，若点C及BC中点D都在反比例函数y= $\frac{k}{x}$ （k<0，x<0）图象上，则k的值为（）

A、-3 B、-4 C、-6 D、-8

查看试题解析
12. 若点A（－3，2）关于原点对称的点是点B，点B关于x轴对称的点是点C，则点C的坐标是（）

A、（3，2） B、（－3，2） C、（3，－2） D、（－2，3）

查看试题解析
13. 如图，圆的四条半径分别是OA，OB，OC，OD，其中点O，A，B在同一条直线上，若∠AOD=90°，∠AOC=3∠BOC，那么圆被四条半径分成的四个扇形的面积的比是（）

A、1：2：2：3 B、3：2：2：3 C、4：2：2：3 D、1：2：2：1

查看试题解析
14. 半径为1的⊙O中，120°的圆心角所对的弦长是（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
15.
如图，⊙O的半径为1，弦AB=1，点P为优弧AB上一动点，AC⊥AP交直线PB于点C，则△ABC的最大面积是（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{4}$

查看试题解析
16. 如图，正方形ABCD中，点E是AD边的中点，BD，CE交于点H，BE、AH交于点G，则下列结论：①∠ABE=∠DCE；②AG⊥BE；③S△BHE=S△CHD；④∠AHB=∠EHD。其中正确的是（）

A、①③ B、①②③④ C、①②③ D、①③④

查看试题解析

二、填空题

17. 在半径为6cm的圆中，60°的圆心角所对的扇形面积等于cm²（结果保留π）。

查看试题解析
18. 数轴上有两个实数a，b，且a>0，b<0，a+b<0，则四个数a，b，-a，-b中最大的是。

查看试题解析
19. 如图，△ABC中，∠C=90°，AC=BC，AD=16cm，BE=12cm，点P是斜边AB的中点．有一把直角尺MPN，将它的顶点与点P重合，将此直角尺绕点P旋转，与两条直角边AC和CB分别交于点D和点E．则线段PD和PE的数量关系为，线段DE= cm。

查看试题解析

三、解答题

20. 计算．

(1)、 $- 1^{4} - (\frac{1}{3} - \frac{3}{14} - 1 \frac{2}{7}) \times (- 42)$

(2)、 $\frac{\cot 45 ° + \tan 60 °}{2 (\sin 60 ° - \cos 60 °)}$ -cot30°

查看试题解析
21. 先化简后求值：

(1)、先化简 $(\frac{x^{2}}{x + 1} - x + 1) \div \frac{x + 2}{x^{2} + 2 x + 1}$ ，再从-1，+1，-2中选择合适的x值代入求值。

(2)、若关于x的分式方程 $\frac{x + m}{x - 2} + \frac{3 m}{4 - 2 x}$ =3的解为正实数，求实数m的取值范围。

查看试题解析
22. 如图，已知点A，B的坐标分别为（0，0）、（2，0），将△ABC绕C点按顺时针方向旋转90°得到△A₁B₁C.

(1)、画出△A₁B₁C；

(2)、A的对应点为A₁ ，写出点A₁的坐标；

(3)、求出B旋转到B₁的路线长.

查看试题解析
23. 在△ABC中，AD平分∠BAC，E是BC上一点，BE=CD，EF∥AD交AB于F点，交CA的延长线于P，CH∥AB交AD的延长线于点H，

(1)、求证：△APF是等腰三角形；

(2)、猜想AB与PC的大小有什么关系？证明你的猜想。

查看试题解析
24. 某商场出售一款速干毛巾，其成本为20元/条，销售中发现，该商品每天的销售量y（条）与销售单价x（元/条）之间存在如图所示的关系。

(1)、请求出y与x的函数关系式；

(2)、该款速干毛巾销售单价定为多少元时，每天销售利润最大？最大利润是多少元？

(3)、近期武汉爆发了“新型冠状病毒”疫情，该商场店主决定从每天获得的利润中抽出200元捐赠给武汉，为了保证捐款后每天剩余利润不低于550元，如何确定该款速干毛巾的销售单价？

查看试题解析
25. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连接AC，过 $\overset{⌢}{B D}$ 上一点E作EG∥AC交CD的延长线于点G，连接AE交CD于点F，且EG=FG．

(1)、求证：EG是⊙O的切线；

(2)、延长AB交GE的延长线于点M，若AH=2， $C H = 2 \sqrt{2}$ ，求OM的长．

查看试题解析
26. 如图，抛物线y= $\frac{1}{2}$ x²+bx+c与直线y= $\frac{1}{2}$ x+3交于A，B两点，交x轴于C、D两点，连接AC、BC，已知A（0，3），C（-3，0）。

(1)、求抛物线的解析式；

(2)、在抛物线对称轴l上找一点M，使|MB-MD|的值最大，并求出这个最大值；

(3)、点P为y轴右侧抛物线上一动点，连接PA，过点P作PO⊥PA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与△ABC相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由。

查看试题解析