广东省2020年中考数学一模试卷
试卷更新日期:2020-05-26 类型:中考模拟
一、选择题
-
1. 2019的倒数是( )A、 2019 B、-2019 C、 D、2. 下列计算正确的是( )A、x·x²=x² B、(xy)²=xy² C、x²+x²=x4 D、(x²)3=x63. 一组数据1,1,4,3,6的平均数和众数分别是( )
A、1,3 B、3,1 C、3,3 D、3,44. 一元二次方程x²+2x-4=0的根的情况为( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定5. 若两个相似三角形的面积之比为1:4,则它们的周长之比为( )A、1:4 B、1:2 C、2:1 D、1:166. 如图,点在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )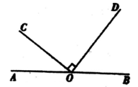 A、36° B、54° C、64° D、72°7. 在平面直角坐标系中,点P(2,3)关于x轴的对称点的坐标是( )A、(-2,-3) B、(2,-3) C、(-2,3) D、(3,2)8. 已知平行四边形ABCD中,∠B=4∠A,则∠C=( )A、18° B、36° C、72° D、144°9. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=( )
A、36° B、54° C、64° D、72°7. 在平面直角坐标系中,点P(2,3)关于x轴的对称点的坐标是( )A、(-2,-3) B、(2,-3) C、(-2,3) D、(3,2)8. 已知平行四边形ABCD中,∠B=4∠A,则∠C=( )A、18° B、36° C、72° D、144°9. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=( )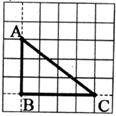 A、 B、 C、 D、10. 某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )A、
A、 B、 C、 D、10. 某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )A、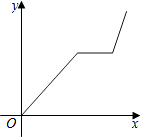 B、
B、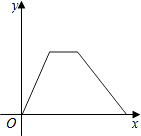 C、
C、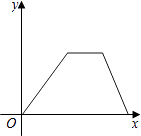 D、
D、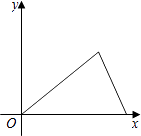
二、填空题
-
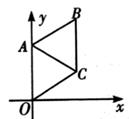
11. 4的平方根是12. 二次函数y=2(x-5)²+3的顶点坐标是。13. 3x-1≤3-x的解集是。14. 菱形的两条对角线的长分别为6和8,则这个菱形的周长为.15. 已知圆柱体的底面半径为3cm,高为4cm,则圆柱体的侧面积为。16. 如图,在平面直角坐标系中,菱形OABC的一个顶点在原点O处,且∠AOC=60°,点A的坐标是(0,4),则直线AC的表达式是。
 17. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE。若AB的长为2,则FM的长为。
17. 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE。若AB的长为2,则FM的长为。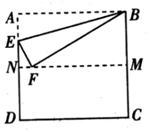
三、解答题一
-
18. 计算: + -19. 先化简,再求值:(1+x)(1-x)+x(x+2)-1,其中x= 。20. 如图,在△ABC中,AB=AC,∠ABC=72°,
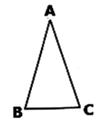 (1)、用直尺和圆规作△ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法)(2)、在(1)中作出∠ABC的平分线BD后,求∠ADB的度数。
(1)、用直尺和圆规作△ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法)(2)、在(1)中作出∠ABC的平分线BD后,求∠ADB的度数。四、解答题二
-
21. 从广州去某市,可乘坐普通火车或高铁,已知高铁的行驶路程是400千米,普通火车的行驶路程是高铁的行程的1.3倍。(1)、求普通火车的行驶路程;(2)、若高铁的平均速度(千米/时)是普通火车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通火车所需时间缩短3小时,求高铁的平均速度。22. 如图,在平行四边形ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F。
 (1)、求证:△ADE≌△CBF;(2)、求证:四边形BFDE为矩形。23. 某校为了解九年级学生2020年适应性考试数学成绩,现从九年级学生中随机抽取部分学生的适应性考试数学成绩,按A,B,C,D四个等级进行统计,并将统计结果绘制成如图所示不完整的统计图。请根据统计图中的信息解答下列问题:
(1)、求证:△ADE≌△CBF;(2)、求证:四边形BFDE为矩形。23. 某校为了解九年级学生2020年适应性考试数学成绩,现从九年级学生中随机抽取部分学生的适应性考试数学成绩,按A,B,C,D四个等级进行统计,并将统计结果绘制成如图所示不完整的统计图。请根据统计图中的信息解答下列问题: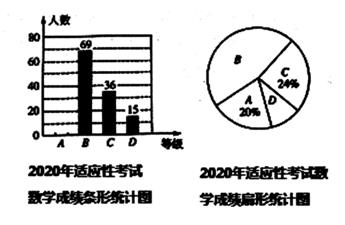
(说明:A等级:135分-150分,B等级:120分-135分,C等级:90分-120分,D等级:0分-90分)
(1)、此次抽查的学生人数为。(2)、把条形统计图和扇形统计图补充完整;(3)、若该校九年级有学生1200人,请估计在这次适应性考试中达到B等级以上的人数。五、解答题三
-
24. 如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F。
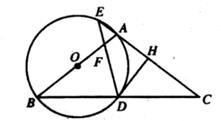 (1)、求证:DH是⊙O的切线;(2)、若A为EH的中点,求 的值;(3)、若EA=EF=1,求⊙O的半径。25. 如图,抛物线C1:y=x²-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。点P为线段BC上一点,过点P作直线l⊥x轴于点F,交抛物线C1于点E。
(1)、求证:DH是⊙O的切线;(2)、若A为EH的中点,求 的值;(3)、若EA=EF=1,求⊙O的半径。25. 如图,抛物线C1:y=x²-2x-3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C。点P为线段BC上一点,过点P作直线l⊥x轴于点F,交抛物线C1于点E。 (1)、求A,B,C三点的坐标;(2)、当点P在线段BC上运动时,求线段PE长的最大值;(3)、当PE取最大值时,把抛物线C1向右平移得到抛物线C2 , 抛物线C2与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线C1应向右平移几个单位长度可得到抛物线C2?
(1)、求A,B,C三点的坐标;(2)、当点P在线段BC上运动时,求线段PE长的最大值;(3)、当PE取最大值时,把抛物线C1向右平移得到抛物线C2 , 抛物线C2与线段BE交于点M,若直线CM把△BCE的面积分为1:2两部分,则抛物线C1应向右平移几个单位长度可得到抛物线C2?