黑龙江省哈尔滨市2020年中考数学六模试卷
试卷更新日期:2020-05-26 类型:中考模拟
一、选择题
-
1. 我市4月份某天的最高气温是8℃,最低气温是-2℃,那么这天的温差是( )A、-2℃ B、2℃ C、-8℃ D、10℃2. 下列运算正确的是( )A、a3·a²=a6 B、(ab3)²=a2b5 C、(a-b)²=a²-b² D、5a-3a=2a3. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图是由四个小正方体叠成的一个立体图形,那么它的俯视图为( )
4. 如图是由四个小正方体叠成的一个立体图形,那么它的俯视图为( )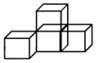 A、
A、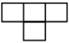 B、
B、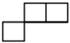 C、
C、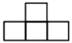 D、
D、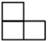 5. 已知反比例函数y= 的图象位于二、四象限,则k的取值范围是( )A、k>2 B、k≥2 C、k≤2 D、k<26. 如图,在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树的坡面上的距离AB为( )米。
5. 已知反比例函数y= 的图象位于二、四象限,则k的取值范围是( )A、k>2 B、k≥2 C、k≤2 D、k<26. 如图,在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树的坡面上的距离AB为( )米。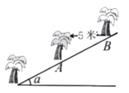 A、5cosα B、 C、5sinα D、7. 抛物线y=(x+3)²+4的顶点坐标为( )A、(-3,4) B、(3,4) C、(4,3) D、(4, -3)8. 如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B'位置,点A落在A'位置,若AC⊥A'B',则∠BAC的度数是( )
A、5cosα B、 C、5sinα D、7. 抛物线y=(x+3)²+4的顶点坐标为( )A、(-3,4) B、(3,4) C、(4,3) D、(4, -3)8. 如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B'位置,点A落在A'位置,若AC⊥A'B',则∠BAC的度数是( )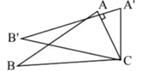 A、50° B、60° C、70° D、80°9. 某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,设安排m名工人生产螺钉,则下面所列方程正确的是( )A、2×1000(26-m)=800m B、1000×(13-m)=800m C、1000×(26-m)=2×800m D、1000×(26-m)=800m10. 如图,点G、F分别是△ACD的边AC、CD上的点,AD的延长线与GF的延长线相交于点B,DE∥AC交GB于点E,则下列结论错误的是( )
A、50° B、60° C、70° D、80°9. 某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,设安排m名工人生产螺钉,则下面所列方程正确的是( )A、2×1000(26-m)=800m B、1000×(13-m)=800m C、1000×(26-m)=2×800m D、1000×(26-m)=800m10. 如图,点G、F分别是△ACD的边AC、CD上的点,AD的延长线与GF的延长线相交于点B,DE∥AC交GB于点E,则下列结论错误的是( )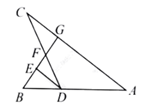 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共计30分)
-
11. 把9200000用科学记数法表示为。12. 在函数y= 中,自变量x的取值范围是。13. 计算: =。14. 把多项式2a3-4a²+2a分解因式的结果是。15. 不等式组 的整数解是。16. 已知一个扇形的面积是15π,圆心角为150°,则此扇形的弧长为。17. 如图,AB为⊙O的直径,点C在⊙O上,∠ACB的平分线交⊙O于点D,连接AD,若∠CAB=30°,则∠CAD的度数为。
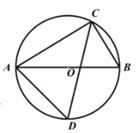 18. 一个不透明的袋子中有4个分别标有数字-6,2,4,-1的球,这些球除所标的数字不同外其他都相同,若从袋子中随机摸出两个球,则这两个球上的两个数字之积为负数的概率是。19. 已知正方形ABCD的边长为3,点P是直线AD上一点,且AD=3AP,连接BP,过点P做BP的垂线交直线CD于点Q,则线段DQ的长为。20. 如图,在Rt△BEG中,∠BEG=90°,ED平分∠BEG,点H、F在EG上,∠CFG=2∠EDH,∠EBG=∠DEB+∠EDH,BD=CD=CG=2,则CF的长为。
18. 一个不透明的袋子中有4个分别标有数字-6,2,4,-1的球,这些球除所标的数字不同外其他都相同,若从袋子中随机摸出两个球,则这两个球上的两个数字之积为负数的概率是。19. 已知正方形ABCD的边长为3,点P是直线AD上一点,且AD=3AP,连接BP,过点P做BP的垂线交直线CD于点Q,则线段DQ的长为。20. 如图,在Rt△BEG中,∠BEG=90°,ED平分∠BEG,点H、F在EG上,∠CFG=2∠EDH,∠EBG=∠DEB+∠EDH,BD=CD=CG=2,则CF的长为。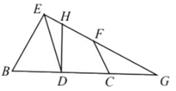
三、解答题
-
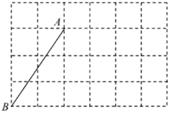
21. 先化简,再求代数式 的值,其中x=sin45°-2cos60°22. 如图,在小正方形边长均为1的方格纸中有线段AB,点A、B均在小正方形的顶点上。
 (1)、以AB为一边画Rt△ABC(点C在小正方形的顶点上),且△ABC的面积为 ;(2)、在(1)的条件下,以AC为一边作△ACD(点D在小正方形的顶点上),使tan∠CAD= ,tan∠ADC=2,直接写出△ACD的周长。23. 为了解中考体育科目训练情况,某区从全区九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图。请根据统计图中的信息解答下列问题:
(1)、以AB为一边画Rt△ABC(点C在小正方形的顶点上),且△ABC的面积为 ;(2)、在(1)的条件下,以AC为一边作△ACD(点D在小正方形的顶点上),使tan∠CAD= ,tan∠ADC=2,直接写出△ACD的周长。23. 为了解中考体育科目训练情况,某区从全区九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图。请根据统计图中的信息解答下列问题: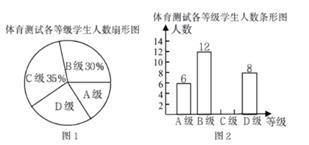 (1)、求本次抽样测试的学生人数是多少?(2)、通过计算将条形统计图补充完整;(3)、该区九年级有学生6000名,如果全部参加这次中考体育科目测试,请估计优秀的人约有多少人?24. 如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,BE=AF,
(1)、求本次抽样测试的学生人数是多少?(2)、通过计算将条形统计图补充完整;(3)、该区九年级有学生6000名,如果全部参加这次中考体育科目测试,请估计优秀的人约有多少人?24. 如图,BD是△ABC的角平分线,点E,F分别在BC、AB上,且DE∥AB,BE=AF, (1)、如图1,求证:AD=EF;(2)、如图2,过A做BD的平行线交EF的延长线于点H,若∠ABC=60°,直接写出图中等于30°的所有角。25. 某学校在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元。(1)、求购买一个甲种足球、一个乙种足球各需多少元?(2)、为响应“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2894元,那么这所学校至少可购买多少个甲种足球?26. CA、CB为⊙O的切线,切点分别为点A、B,延长AO交⊙O于点D,连接AB、CO,AB与CO交于点M,
(1)、如图1,求证:AD=EF;(2)、如图2,过A做BD的平行线交EF的延长线于点H,若∠ABC=60°,直接写出图中等于30°的所有角。25. 某学校在商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍,且购买一个乙种足球比购买一个甲种足球多花20元。(1)、求购买一个甲种足球、一个乙种足球各需多少元?(2)、为响应“足球进校园”的号召,这所学校决定再次购买甲、乙两种足球共50个,恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%,如果此次购买甲、乙两种足球的总费用不超过2894元,那么这所学校至少可购买多少个甲种足球?26. CA、CB为⊙O的切线,切点分别为点A、B,延长AO交⊙O于点D,连接AB、CO,AB与CO交于点M, (1)、如图1,求证:∠ACB=2∠BAO;(2)、如图2,连接BD,求证:BD=2OM;(3)、如图3,在(2)的条件下,F为OD上一点,连接FM并延长交AC于点H,连接BH,若DF=2OF,HM=3,tan∠ACB= ,求线段BH的长。27. 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax²-2ax-3a交x轴于A、B两点,交y轴于点C,连接BC,且OB=OC。
(1)、如图1,求证:∠ACB=2∠BAO;(2)、如图2,连接BD,求证:BD=2OM;(3)、如图3,在(2)的条件下,F为OD上一点,连接FM并延长交AC于点H,连接BH,若DF=2OF,HM=3,tan∠ACB= ,求线段BH的长。27. 如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax²-2ax-3a交x轴于A、B两点,交y轴于点C,连接BC,且OB=OC。 (1)、求抛物线的解析式;(2)、如图2,D为第一象限内抛物线上一点,过D做DT⊥x轴交x轴于T,交BC于点K,设D点横坐标为m,线段DK的长为d,求d与m之间的关系式;(3)、如图3,在(2)的条件下,D在对称轴右侧,Q、H为直线DT上一点,Q点纵坐标为4,H在第四象限内,且QD=TH,过D做x轴的平行线交抛物线于点E,连接EQ交抛物线于点R,连接RH,tan∠ERH=2,求点D的坐标。
(1)、求抛物线的解析式;(2)、如图2,D为第一象限内抛物线上一点,过D做DT⊥x轴交x轴于T,交BC于点K,设D点横坐标为m,线段DK的长为d,求d与m之间的关系式;(3)、如图3,在(2)的条件下,D在对称轴右侧,Q、H为直线DT上一点,Q点纵坐标为4,H在第四象限内,且QD=TH,过D做x轴的平行线交抛物线于点E,连接EQ交抛物线于点R,连接RH,tan∠ERH=2,求点D的坐标。