甘肃秦安县2020年中考数学模拟试卷
试卷更新日期:2020-05-26 类型:中考模拟
一、选择题
-
1. 若x与3互为相反数,则|x+3|等于( )A、0 B、1 C、2 D、32.
如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )
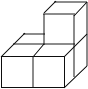 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、a3+a2=2a5 B、a6÷a2=a3 C、(a+b)2=a2+b2 D、(-2a3)2=4a64. 根据国家财政部有关数据,自新型冠状病毒感染的肺炎疫情发生以来,截止2月13日,全国各级财政共计投入805.5亿元用于疫情防控。其中数据805.5亿用科学记数法表示为( )A、805.5×108 B、8.055×1010 C、8.055×1011 D、0.8055×10115. 观察下列图案,既是轴对称图形又是中心对称图形的共有( )
3. 下列计算正确的是( )A、a3+a2=2a5 B、a6÷a2=a3 C、(a+b)2=a2+b2 D、(-2a3)2=4a64. 根据国家财政部有关数据,自新型冠状病毒感染的肺炎疫情发生以来,截止2月13日,全国各级财政共计投入805.5亿元用于疫情防控。其中数据805.5亿用科学记数法表示为( )A、805.5×108 B、8.055×1010 C、8.055×1011 D、0.8055×10115. 观察下列图案,既是轴对称图形又是中心对称图形的共有( )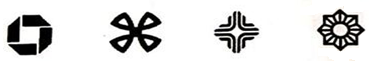
A、4个 B、3个 C、2个 D、1个6. 抛物线y=2(x+1)2-3的顶点坐标是( )A、(1,-3) B、(1,3) C、(-1,-3) D、(-1,3)7. 在正方形网格中,△ABC的位置如图所示,则cosB的值为( )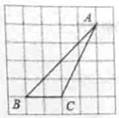 A、 B、 C、 D、8. 已知分式 的值为0,那么x的值是( )A、-2 B、-1 C、1 D、1或-29. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ,则S阴影=( )
A、 B、 C、 D、8. 已知分式 的值为0,那么x的值是( )A、-2 B、-1 C、1 D、1或-29. 如图,AB是圆O的直径,弦CD⊥AB,∠BCD=30°,CD=4 ,则S阴影=( )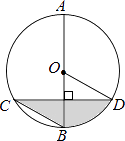 A、2π B、 π C、 π D、 π10. 如图,边长为2的等边△ABC和边长为1的等边△A'B'C',它们的边B'C',BC位于同一条直线L上,开始时,点C'与B重合,△ABC固定不动,然后把△A'B'C'自左向右沿直线L平移,移出△ABC外(点B'与C重合)停止,设△A'B'C'平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )
A、2π B、 π C、 π D、 π10. 如图,边长为2的等边△ABC和边长为1的等边△A'B'C',它们的边B'C',BC位于同一条直线L上,开始时,点C'与B重合,△ABC固定不动,然后把△A'B'C'自左向右沿直线L平移,移出△ABC外(点B'与C重合)停止,设△A'B'C'平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )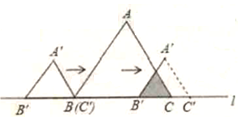 A、
A、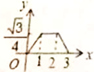 B、
B、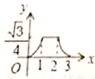 C、
C、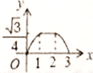 D、
D、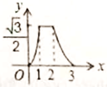
二、填空题
-
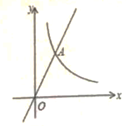
11. 若式子 有意义,则x的取值范围是 .12. 分解因式: -x= .13. 规定一种运算“*”,a*b= a- b,则方程x*2=1*x的解为。14. 如图,直线y1=kx(k≠0)与双曲线y2= (x>0)交于点A(1,a),则y1>y2的解集为。
 15.
15.观察下列的“蜂窝图”

则第n个图案中的“
 ”的个数是 . (用含有n的代数式表示)16. 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A'的位置,若OB= ,tan∠BOC= ,则点A'的坐标为。
”的个数是 . (用含有n的代数式表示)16. 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连接OB,将纸片OABC沿OB折叠,使点A落在点A'的位置,若OB= ,tan∠BOC= ,则点A'的坐标为。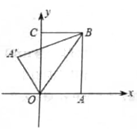 17. 如图所示,正方形ABCD的边长为8,E是边BC上的一点,且BE=2,P是对角线AC上的一动点,连接PB、PE,当点P在AC上运动时,△PBE周长的最小值是。
17. 如图所示,正方形ABCD的边长为8,E是边BC上的一点,且BE=2,P是对角线AC上的一动点,连接PB、PE,当点P在AC上运动时,△PBE周长的最小值是。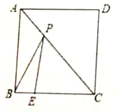 18. 如图是抛物线y1=ax2+bx+c(a≠0) 的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①abc>0;②方程ax2+bx+c=3有两个相等的实数根;③抛物线与x轴的另一个交点是(-1,0);④当1<x<4时,有y2>y1;⑤x(ax+b)≤a+b,其中正确的结论是。(只填写序号)
18. 如图是抛物线y1=ax2+bx+c(a≠0) 的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①abc>0;②方程ax2+bx+c=3有两个相等的实数根;③抛物线与x轴的另一个交点是(-1,0);④当1<x<4时,有y2>y1;⑤x(ax+b)≤a+b,其中正确的结论是。(只填写序号)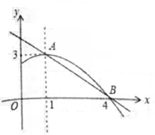
三、解答题
-
19. 计算-14+ sin60°+ -20. 先化简,再求值: ,其中x=2sin60°-121. 在下面的网格中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(-3,0),(-1,-1)。
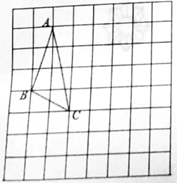 (1)、请在图中画出平面直角坐标系,并直接写出点A的坐标。(2)、将△ABC绕着坐标原点顺时针旋转90°,画出旋转后的△A'B'C'。(3)、写出在上述旋转过程中,点A所经过的路径长。22. 为了保障人民群众的身体健康,在新型冠状病毒感染的肺炎疫情防控期国家有关部门加强对口罩等防疫物资的监管,严厉打击防疫物资生产领域的违法行为。在对某医药超市进行抽查时,随机抽取了5只独立包装的KN95口罩。经检测,这5只口罩中,有1只不合格品和4只合格品。(1)、从这5只口罩中随机抽取1只,抽到不合格品的概率是多少?(2)、用画树状图或列表的方法,求从这5只口罩中随机抽取2只,抽到不合格品的概率。23. 如图所示,一次函数y=kx+b与反比例函数y= 的图象交于A(2,4),B(-4,n)两点。
(1)、请在图中画出平面直角坐标系,并直接写出点A的坐标。(2)、将△ABC绕着坐标原点顺时针旋转90°,画出旋转后的△A'B'C'。(3)、写出在上述旋转过程中,点A所经过的路径长。22. 为了保障人民群众的身体健康,在新型冠状病毒感染的肺炎疫情防控期国家有关部门加强对口罩等防疫物资的监管,严厉打击防疫物资生产领域的违法行为。在对某医药超市进行抽查时,随机抽取了5只独立包装的KN95口罩。经检测,这5只口罩中,有1只不合格品和4只合格品。(1)、从这5只口罩中随机抽取1只,抽到不合格品的概率是多少?(2)、用画树状图或列表的方法,求从这5只口罩中随机抽取2只,抽到不合格品的概率。23. 如图所示,一次函数y=kx+b与反比例函数y= 的图象交于A(2,4),B(-4,n)两点。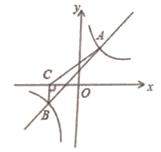 (1)、分别求出一次函数与反比例函数的表达式;(2)、过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积。24. 近年来,我国持续的大面积的雾霾天气让环境和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解。根据调查统计结果,绘制了如图所示的不完整的三种统计图表。
(1)、分别求出一次函数与反比例函数的表达式;(2)、过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积。24. 近年来,我国持续的大面积的雾霾天气让环境和健康问题成为焦点,为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解。根据调查统计结果,绘制了如图所示的不完整的三种统计图表。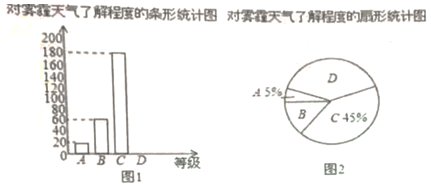
对雾霾所了解程度的统计表:
对雾霾的了解程度
百分比
A.非常了解
5%
B.比较了解
15%
C.基本了解
45%
D.不了解
n
请结合统计图表,回答下列问题
(1)、本次参与调查的学生共有人,n=;(2)、扇形统计图中D部分扇形所对应的圆心角是度;(3)、请补全条形统计图25. 如图,在正方形ABCD中,点E、F分别在边AB、BC上,∠ADE=∠CDF。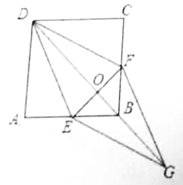 (1)、求证:AE=CF;(2)、连结DB交CF于点O,延长OB至点G,使OG=OD,连结EG、FG,判断四边形DEGF是否是菱形,并说明理由。26. 某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.(1)、求出y与x的函数关系式,并写出自变量x的取值范围.(2)、当销售单价为多少元时,销售这种童装每月可获利1800元?(3)、当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?27. 如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD。连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N。
(1)、求证:AE=CF;(2)、连结DB交CF于点O,延长OB至点G,使OG=OD,连结EG、FG,判断四边形DEGF是否是菱形,并说明理由。26. 某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.(1)、求出y与x的函数关系式,并写出自变量x的取值范围.(2)、当销售单价为多少元时,销售这种童装每月可获利1800元?(3)、当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?27. 如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD。连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N。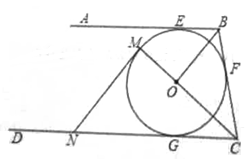 (1)、求证:MN是⊙O的切线;(2)、当OB=6cm,OC=8cm时,求⊙O的半径及MN的长。28. 如图,在平面直角坐标系中,抛物线y=- x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=- x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7。
(1)、求证:MN是⊙O的切线;(2)、当OB=6cm,OC=8cm时,求⊙O的半径及MN的长。28. 如图,在平面直角坐标系中,抛物线y=- x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=- x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7。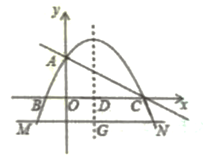 (1)、求此抛物线的解析式。(2)、求点N的坐标。(3)、过点A的直线与抛物线交于点F,当tan∠FAC= 时,求点F的坐标。
(1)、求此抛物线的解析式。(2)、求点N的坐标。(3)、过点A的直线与抛物线交于点F,当tan∠FAC= 时,求点F的坐标。