浙江省温州市六校2020年数学中考模拟联考试
试卷更新日期:2020-05-26 类型:中考模拟
一、选择题(本题有10小题,每小题4分,共40分.)
-
1. 在|-2|,-(+2),2-1 , 0这四个数中,最小的数是( )A、|-2| B、-(+2) C、0 D、2-12. 近期,新型冠状病毒感染肺炎的疫情在全国蔓延,全国人民团结一致,全力抗击新型冠状病毒感染肺炎.社会各界人士积极捐款。截止2月5日中午12点,武汉市慈善总会接收捐赠款约3230000000元。将3230000000用科学记数法表示应为( )A、323×107 B、32.3×108 C、3.23×109 D、3.23×10103.
如图物体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,一个圆形飞镖板被分为四个圆心角相等的扇形,若大圆半径为2,小圆半径为1,则阴影部分的面积为( )
4. 如图,一个圆形飞镖板被分为四个圆心角相等的扇形,若大圆半径为2,小圆半径为1,则阴影部分的面积为( )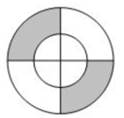 A、π B、 π C、3π D、 π5. 如图,小猫在5×5的地板砖上行走,并随机停留在某一块方砖上,则它停留在阴影方砖上的概率是( )
A、π B、 π C、3π D、 π5. 如图,小猫在5×5的地板砖上行走,并随机停留在某一块方砖上,则它停留在阴影方砖上的概率是( )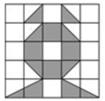 A、 B、 C、 D、6. 下列抛物线中,其顶点在反比例函数y= 的图象上的是( )A、y=(x-4)2+3 B、y=(x-4)2-3 C、y=(x+2)2+1 D、y=(x+2)2-17. 如图,小明将一张长为20cm,宽为15cm的长方形纸(AE>DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为( )
A、 B、 C、 D、6. 下列抛物线中,其顶点在反比例函数y= 的图象上的是( )A、y=(x-4)2+3 B、y=(x-4)2-3 C、y=(x+2)2+1 D、y=(x+2)2-17. 如图,小明将一张长为20cm,宽为15cm的长方形纸(AE>DE)剪去了一角,量得AB=3cm,CD=4cm,则剪去的直角三角形的斜边长为( )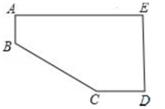 A、5cm B、12cm C、16cm D、20cm8. 如图,在平面直角坐标系中,在x轴、y轴的半轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于 AB长为半径作弧,两弧交于点C.若点C的坐标为(m-1,2n),则m与n的关系为( )
A、5cm B、12cm C、16cm D、20cm8. 如图,在平面直角坐标系中,在x轴、y轴的半轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于 AB长为半径作弧,两弧交于点C.若点C的坐标为(m-1,2n),则m与n的关系为( )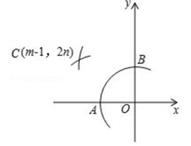 A、m+2n=1 B、m-2n=1 C、2n-m=1 D、n-2m=19. 已知二次函数y=x²-2x+2(其中x是自变量),当0≤x≤a时,y的最大值为2,y的最小值为1,则a的值为( )A、a=1 B、1≤a<2 C、1<a≤2 D、1≤a≤210. 点C是半径为1的半圆弧AB的一个三等分点,分别以弦AC、BC为直径向外侧作2个半圆,点D、E也分别是2半圆弧的三等分点,再分别以弦AD、DC、CE、BE为直径向外侧作4个半圆。则图中阴影部分(4个新月牙形)的面积和是( )
A、m+2n=1 B、m-2n=1 C、2n-m=1 D、n-2m=19. 已知二次函数y=x²-2x+2(其中x是自变量),当0≤x≤a时,y的最大值为2,y的最小值为1,则a的值为( )A、a=1 B、1≤a<2 C、1<a≤2 D、1≤a≤210. 点C是半径为1的半圆弧AB的一个三等分点,分别以弦AC、BC为直径向外侧作2个半圆,点D、E也分别是2半圆弧的三等分点,再分别以弦AD、DC、CE、BE为直径向外侧作4个半圆。则图中阴影部分(4个新月牙形)的面积和是( )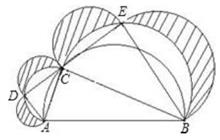 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题5分,共30分)
-
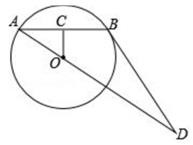
11. 若a2+2a=4,则(a+1)2=。12. 不等式组 的解集为。13. 一组数据:23,27,20,18,x,16.它们的平均数是21,则中位数为。14. 如图,在⊙O中过O作OC⊥AB于C,连接AO并延长,交过B点的⊙O的切线于D点,若AB=8,BD=12,OC=3,则AD= 。
 15. 如图,矩形ABCD中,AB=10,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,当OE=OD时,AP的长为。
15. 如图,矩形ABCD中,AB=10,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,当OE=OD时,AP的长为。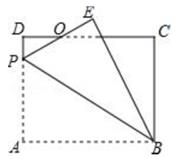 16. 图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD”。某家装厂设计的折叠床是AB=8cm,BC=16cm,①此时CD应该是多长。②折叠时,当AB⊥BC'时,sinD'=。
16. 图1是一张可以折叠的小床展开后支撑起来放在地面的示意图,此时点A、B、C在同一直线上,且∠ACD=90°,图2是小床支撑脚CD折叠的示意图,在折叠过程中,△ACD变形为四边形ABC'D',最后折叠形成一条线段BD”。某家装厂设计的折叠床是AB=8cm,BC=16cm,①此时CD应该是多长。②折叠时,当AB⊥BC'时,sinD'=。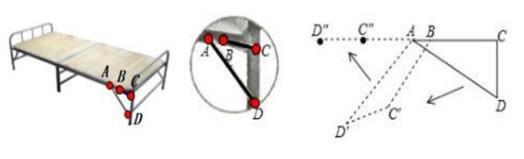
三、解答题(本题有8小题,共80分。)
-
17.(1)、计算:(π-3.14)0-2 cos30°+( )-2(2)、化简:18. 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
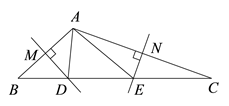 (1)、若BC=5,求△ADE的周长.(2)、若∠BAD+∠CAE=60°,求∠BAC的度数.19. 新冠疫情期间,某学校为了更好地帮助学生进行网上学习,随机调查了本校部分初三学生的学习成果。并将其分为A,B,C,D四种类型(分别对应优、良、合格、待合格)。现根据调查的数据绘制成如下的条形统计图和扇形统计图。
(1)、若BC=5,求△ADE的周长.(2)、若∠BAD+∠CAE=60°,求∠BAC的度数.19. 新冠疫情期间,某学校为了更好地帮助学生进行网上学习,随机调查了本校部分初三学生的学习成果。并将其分为A,B,C,D四种类型(分别对应优、良、合格、待合格)。现根据调查的数据绘制成如下的条形统计图和扇形统计图。请根据以上不完整的统计图提供的信息,解答下列问题:
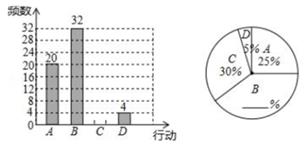 (1)、该校共调查了名同学的学习成果?(2)、补全条形统计图和扇形统计图;(3)、若该校初三一共有500名学生。开学后学校计划把C和D等级的同学平均分成了四个班级,利用课后时间来巩固网课内容。已知小红和小玲都在C,D两组里面,问他们分到一个班进行巩固学习的概率有多大。(利用树状图或表格解答)20. 6×6的方格图中,按要求作格点三角形ABC。
(1)、该校共调查了名同学的学习成果?(2)、补全条形统计图和扇形统计图;(3)、若该校初三一共有500名学生。开学后学校计划把C和D等级的同学平均分成了四个班级,利用课后时间来巩固网课内容。已知小红和小玲都在C,D两组里面,问他们分到一个班进行巩固学习的概率有多大。(利用树状图或表格解答)20. 6×6的方格图中,按要求作格点三角形ABC。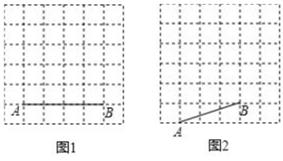 (1)、在图1中,作等腰直角△ABC,使得∠BAC=45°;(画出一个即可)(2)、在图2中,作平行四边形ABCD,使得∠BAD=45°。21. 已知:如图,以BC为直径作⊙O,AC切⊙O于点C,连接AB,交⊙O于点D,E为 上一点,CE、DB交于点F且AC=AF。
(1)、在图1中,作等腰直角△ABC,使得∠BAC=45°;(画出一个即可)(2)、在图2中,作平行四边形ABCD,使得∠BAD=45°。21. 已知:如图,以BC为直径作⊙O,AC切⊙O于点C,连接AB,交⊙O于点D,E为 上一点,CE、DB交于点F且AC=AF。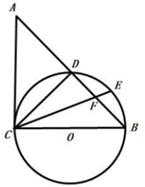 (1)、求证:E为 的中点。(2)、若CF=8,EF=2,求⊙O的半径。22. 如图,已知二次函数y=ax²-2ax+c(a<0)的图象交x轴于A、B两点,交y轴于点C。过点A的直线y=kx+2k(k≠0)与这个二次函数的图象的另一个交点为F,与该图象的对称轴交于点E,与y轴交于点D,且DE=EF。
(1)、求证:E为 的中点。(2)、若CF=8,EF=2,求⊙O的半径。22. 如图,已知二次函数y=ax²-2ax+c(a<0)的图象交x轴于A、B两点,交y轴于点C。过点A的直线y=kx+2k(k≠0)与这个二次函数的图象的另一个交点为F,与该图象的对称轴交于点E,与y轴交于点D,且DE=EF。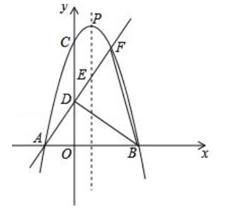 (1)、求点A,点B的坐标,并把c用a表示;(2)、若△BDF的面积为12,求这个二次函数的关系式。23. 温州某一企业原先一次性口罩和防雾霾口罩生产信息如下表:
(1)、求点A,点B的坐标,并把c用a表示;(2)、若△BDF的面积为12,求这个二次函数的关系式。23. 温州某一企业原先一次性口罩和防雾霾口罩生产信息如下表:口罩类型
材料成本(不含人工)
出厂价
产量(一人一天)
一次性口罩
0.1元/个
0.2元/个
2000个
防雾霾口罩
2.5元/个
4元/个
200个
已知该企业有12名工人,工资每人每天150元。该企业原来每天产量共15000个口罩。
(1)、求原先企业安排生产一次性口罩和防雾霾口罩各有多少人。(2)、经一段时间运行,企业发现每天销售的防雾霾口罩,最多只能卖900个。而一次性口罩可以全部销售,市场缺口较大。怎么安排生产口罩的人数可以使该企业每一天获得利润最大。最大利润是多少?(注:没有销售的口罩,作为库存暂时当做不赚不亏)。(3)、在疫情期间,为了配合政府防疫工作,该厂改为全部生产一次性口罩。因为原材料价格暴涨,口罩的材料成本和出厂价分别变为0.6元/个和1元/个。一部分员工因为滞留在外,无法及时回来工作。所以该厂提高了剩余老员工的工资,也招募了几个新员工过来且老员工人数多于新员工。信息如下表:员工类型
每日工资
一次性口罩产量(一人一天)
老员工
300元/天
2000个
新员工
200元/天
1000个
要是该厂的利润达到4000元/天。求该厂留下来的老员工和招募的新员工人数。
24. 在矩形ABCD中,点E是AD上一动点,连结BE,过点E作EF⊥BE,交CD于F,以EF为直径作⊙O。设AE=t。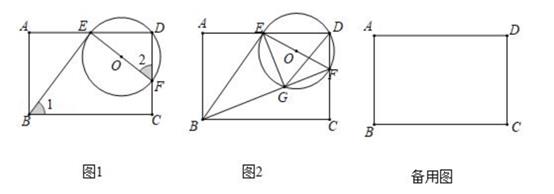 (1)、求证∠1=∠2;(2)、如图2,已知AD=8,连结BF,交⊙O于点G,并连结EG,DG,
(1)、求证∠1=∠2;(2)、如图2,已知AD=8,连结BF,交⊙O于点G,并连结EG,DG,①当AB=6时,若△EGD是以EG为腰的等腰三角形,求t的值;
②连接OC,GC,当tan∠FBC= ,OC∥EG时,求t的值。
(3)、OC交BF于点P,当tan∠1=1,OC∥EG时,记△OFP的面积为S1 , △CGP的面积为S2 , 四边形EGCF的面积为S3 , 请直接写出 的值。