浙江省余姚市2020年初中学业水平模拟考试数学试卷

试卷更新日期：2020-05-26 类型：中考模拟

进入出卷网下载

一、选择题(每小题4分，共40分)

1. 在0， $\sqrt{3}$ ，2，-1这四个数中，最大的数是（）

A、0 B、 $\sqrt{3}$ C、2 D、-1

查看试题解析
2. 下列运算正确的是（）

A、x²+x²=2x⁴ B、x³·x²=x⁵ C、x⁹÷x³=x³ D、(x²)³=x⁵

查看试题解析
3. 据交通运输部统计，受肺炎疫情影响，今年春运1月25日~2月14日，全国共发送旅客2.83亿人次，日均1348万人次，同比分别下降82.3%.将1348万用科学记数法表示为（）

A、1348×10⁴ B、13.48×10⁶ C、1.348×10⁶ D、1.348×10⁷

查看试题解析
4. 在函数y= $\frac{x}{\sqrt{x + 3}}$ 中，自变量x的取值范围是（）

A、x≥-3 B、x≥-3且x≠0 C、x≠0 D、x>-3

查看试题解析
5. 图①是由五个完全相同的小正方体组成的立体图形.将图①中的一个小正方体改变位置后如图②，则三视图发生改变的是（）

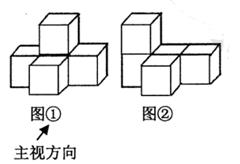A、主视图 B、俯视图 C、左视图 D、主视图、俯视图和左视图都改变

查看试题解析
6. 不等式组 ${\begin{cases} 3 x - 1 > x + 1 \\ 7 - 3 x \geq 1 \end{cases}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形，将其背面朝上放在桌面上，从中随机抽取一张，所抽取的卡片上的图形既是轴对称图形，又是中心对称图形的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
8. 小红同学对数据24，48，23，24，5■，52进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（）

A、平均数 B、中位数 C、方差 D、众数

查看试题解析
9. 如图，将矩形ABCD绕着点A逆时针旋转得到矩形AEFG，点B的对应点E落在边CD上，且DE=EF，若AD= $\sqrt{3}$ ，则 $\overset{⌢}{C F}$ 的长为（）

A、 $\frac{3 π}{8}$ B、 $\frac{3 π}{4}$ C、 $\frac{\sqrt{6} π}{4}$ D、π

查看试题解析
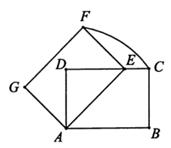10. 在矩形ABCD内，将两张边长分别为a和b(a>b)的正方形纸片按图1，图2两种方式放置(图1，图2中两张正方形纸片均有部分重叠)，矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图2中阴影部分的周长与图1中阴影部分的周长的差为l，若要知道l的值，只要测量图中哪条线段的长（）

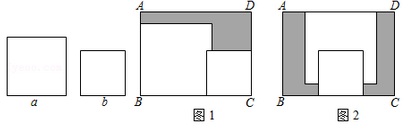A、a B、b C、AD D、AB

查看试题解析

二、填空题(每小题5分，共30分)

11. 分解因式：x²-4y²=。

查看试题解析
12. -64的立方根是。

查看试题解析
13. 已知圆锥的母线和高线的长是一元二次方程x²-8x+15=0的两个根，则圆锥的侧面积为。

查看试题解析
14. 在一次综合社会实践活动中，小东同学从A处出发，要到A地北偏东60°方向的C处，他先沿正东方向走了4千米到达B处，再沿北偏东15°方向走，恰能到达目的地C，如图所示，则A、C两地相距千米。(结果精确到0.1千米，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732)

查看试题解析
15. 如图，在矩形ABCD中，AB=3，BC=4，P是对角线AC上的动点，以点P为圆心，PC长为半径作⊙P。当⊙P与矩形ABCD的边相切时，CP的长为。

查看试题解析
16. 如图，在平面直角坐标系中，△OAB的边OB在x轴的正半轴上，AO=AB，M是边AB的中点，经过点M的反比例函数y= $\frac{k}{x}$ (k>0，x>0)的图象与边OA交于点C，则 $\frac{O C}{O A}$ 的值为。

查看试题解析

三、解答题(本大题有8小题，共80分)

17. 解答下列各题：

(1)、计算：2³+|-3|- $\sqrt{9}$ -π⁰

(2)、解方程： $\frac{x - 2}{x - 3} + 1 = \frac{3}{3 - x}$

查看试题解析
18. 图1，图2都是由边长为1的小等边三角形构成的网格，△ABC为格点三角形，请仅用无刻度直尺在网格中完成下列画图。

(1)、在图1中，画出△ABC中AB边上的中线CM；

(2)、在图2中，画出∠APC，使∠APC=∠ABC，且点P是格点(画出一个即可)。

查看试题解析

19. 某校为了解学生对“防溺水”安全知识的掌握情况，从全校1500名学生中随机抽取部分学生进行测试，并将测试成绩(百分制，得分均为整数)进行统计分析，绘制了如下不完整的频数表和频数直方图。

被抽取的部分学生安全知识测试成绩频数表

组别	成绩x(分)	频数(人)	频率
A组	50≤x<60	6	0.12
B组	60≤x<70	a	0.28
C组	70≤x<80	16	0.32
D组	80≤x<90	10	0.20
E组	90≤x<100	4	0.08

被抽取的部分学生安全知识测试成绩频数直方图

由图表中给出的信息回答下列问题：

(1)、表中的a=：抽取部分学生的成绩的中位数在组；

(2)、把上面的频数直方图补充完整；

(3)、如果成绩达到80分以上(包括80分)为优秀，请估计该校1500名学生中成绩优秀的人数。

查看试题解析

20. 如图，已知二次函数y=-x²+bx+c的图象经过点A(3，1)，点B(0，4)。

(1)、求该二次函数的表达式及顶点坐标；

(2)、点C(m，n)在该二次函数图象上。
①当m=-1时，求n的值；

②当m≤x≤3时，n最大值为5，最小值为1，请根据图象直接写出m的取值范围。

查看试题解析
21. 如图，在 $▱$ ABCD中，对角线AC，BD相交于点O，过点O作BD的垂线与边AD，BC分别交于点E，F，连接BE交AC于点K，连接DF。

(1)、求证：四边形EBFD是菱形；

(2)、若BK=3EK，AE=4，求四边形EBFD的周长。

查看试题解析
22. 小明星期天上午8：00从家出发到离家36千米的书城买书，他先从家出发骑公共自行车到公交车站，等了12分钟的车，然后乘公交车于9：48分到达书城(假设在整个过程中小明骑车的速度不变，公交车匀速行驶，小明家、公交车站、书城依次在一条笔直的公路旁)。如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象，其中线段AB对应的函数表达式为y=kx+6。

(1)、求小明骑公共自行车的速度；

(2)、求线段CD对应的函数表达式：

(3)、求出发时间x在什么范围时，小明离公交车站的路程不超过3千米？

查看试题解析
23. 如图1，平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC，若有PA²+PB²=PC² ，则称点P为△ABC关于点C的勾股点。

(1)、如图2，在4×3的方格纸中，每个小正方形的边长均为1，△ABC的顶点在格点上，请找出所有的格点P，使点P为△ABC关于点A的勾股点。

(2)、如图3，△ABC为等腰直角三角形，P是斜边BC延长线上一点，连接AP，以AP为直角边作等腰直角三角形APD(点A、P、D顺时针排列)，∠PAD=90°，连接DC，DB，求证：点P为△BDC关于点D的勾股点。

(3)、如图4，点E是矩形ABCD外一点，且点C是△ABE关于点A的勾股点，若AD=8，CE=5，AD=DE，求AE的长。

查看试题解析
24. 如图1，直线l：y= $- \frac{1}{2}$ x+4与x轴交于点A，与y轴交于点B，以AB为直线作⊙M，点P为线段OA上一动点(与点O、A不重合)，作PC⊥AB于C，连结BP并延长交⊙O于点D。

(1)、求点A，B的坐标和tan∠BAO的值；

(2)、设 $\frac{B C}{C A}$ =x，tan∠BPO=y。
①当x=1时，求y的值及点D的坐标；

②求y关于x的函数表达式；

(3)、如图2，连接OC，当点P在线段OA上运动时，求OC·PD的最大值。

查看试题解析