浙江省台州市2020年九年级数学中考基础冲刺试卷
试卷更新日期：2020-05-26 类型：中考模拟
一、选择题（每题4分，满分40分）
-
1. 对于单项式 ，下列说法正确的是（ ）A、它与3πa2b不是同类项 B、它的系数是3 C、它是二次单项式 D、它与﹣ 的和是﹣2a2b2. 如图，是一个由若干个小正方体组成的几何体的主视图和左视图，则该几何体最多可由多少个小正方体组合而成？（ ）
A、12个 B、13个 C、14个 D、15个3. 新冠肺炎疫情爆发以来，口罩成为需求最为迫切的防护物资.在这个关键时刻，我国某企业利用自身优势转产口罩，这背后不仅体现出企业强烈的社会责任感，更是我国人民团结一心抗击疫情的决心据悉该企业3月份的口罩日产能已达到500万只，预计今后数月内都将保持同样的产能，则3月份（按31天计算）该企业生产的口罩总数量用科学记数法表示为（ ）A、1.55×107只 B、1.55×108只 C、0.155×109只 D、5×106只4. 在周长为25的三角形中，最短边是x，另一边是2x﹣3，则x的取值范围（ ）
A、 ＜x＜ B、 ＜x＜7 C、3≤x≤7 D、3＜x＜75. 某同学对数据26，36，36，46，5■，52进行统计分析.发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（ ）A、平均数 B、中位数 C、方差 D、众数6. 我国明代数学读本《算法统宗》一书中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托，如果一托为5尺，那么索长（ ）尺.A、25 B、20 C、15 D、107. 如图是某商品标牌的示意图，⊙O与等边△ABC的边BC相切于点C，且⊙O的直径与△ABC的高相等，已知等边△ABC边长为4，设⊙O与AC相交于点E，则AE的长为（ ）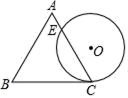
A、 B、1 C、 ﹣1 D、8. 下列说法正确的是（ ）A、对角线互相垂直的四边形是菱形 B、四边相等的四边形是菱形 C、一组对边平行的四边形是平行四边形 D、矩形的对角线互相垂直9. 下列四个命题中，真命题有（ ）①两条直线被第三条直线所截，内错角相等．
②如果∠1和∠2是对顶角，那么∠1=∠2．
③三角形的一个外角大于任何一个内角．
④如果x2＞0，那么x＞0．
A、1个 B、2个 C、3个 D、4个10. 小明遇到这样一个问题：如图，矩形纸片ABCD，AB＝2，BC＝3，现要求将矩形纸片剪两刀后拼成一个与之面积相等的正方形，小明尝试给出了下面四种剪的方法，如图①②③④，图中BE＝ .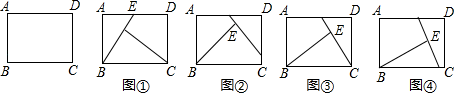
其中剪法正确的是（ ）
A、①② B、①③ C、②③ D、③④二、填空题（每题5分，满分30分）
-
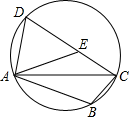
11. 因式分解：ab2﹣2ab+a＝ ．12. 已知3m﹣1和m﹣7是数p的平方根，则p的值为.13. 一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1、2、3、4．随机摸取一个小球然后放回，再随机摸出一个小球，两次取出的小球标号的和等于5的概率是 ．14. 如图，四边形ABCD内接于圆，点B关于对角线AC的对称点E落在边CD上，连接AE.若∠ABC＝115°，则∠DAE的度数为.
15. 有一组数：﹣ ， ，﹣ ， ，﹣ ……请观察这组数的构成规律，用你发现的规律确定第10个数是.16. 如图，在直角三角形ABC中，∠A＝90°，AB＝3，AC＝4，BC＝5，DE∥BC，点A到DE的距离是1，则DE与BC的距离是.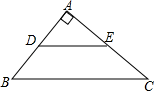
三、解答题
-
17. 计算：（﹣1）3+|1﹣ |+ ﹣
18. 化简求值： ，其中 .19. 高淳固城湖大桥采用H型塔型斜拉桥结构（如甲图），图乙是从图甲抽象出的平面图.测得拉索AB与水平桥面的夹角是45°，拉索CD与水平桥面的夹角是65°，两拉索顶端的距离AC为2米，两拉索底端距离BD为10米，请求出立柱AH的长（结果精确到0.1米）.（参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14）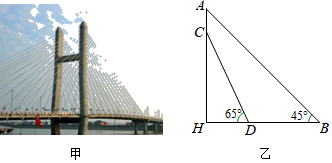
20. 自2017年3月起，成都市中心城区居民用水实行以户为单位的三级阶梯收费办法：第I级：居民每户每月用水18吨以内含18吨每吨收水费a元；
第Ⅱ级：居民每户每月用水超过18吨但不超过25吨，未超过18吨的部分按照第Ⅰ级标准收费，超过部分每吨收水费b元；
第Ⅲ级：居民每户每月用水超过25吨，未超过25吨的部分按照第I、Ⅱ级标准收费，超过部分每吨收水费c元.
设一户居民月用水x吨，应缴水费为y元，y与x之间的函数关系如图所示
(1)、根据图象直接作答：a＝ ， b＝；(2)、求当x≥25时y与x之间的函数关系；(3)、把上述水费阶梯收费办法称为方案①，假设还存在方案②：居民每户月用水一律按照每吨4元的标准缴费，请你根据居民每户月“用水量的大小设计出对居民缴费最实惠的方案.（写出过程）