浙江省台州市临海市一中2020年数学中考一模试卷（5月）
试卷更新日期：2020-05-26 类型：中考模拟
一、选择题：本题共10小题，每小题4分，共40分.
-
1. ﹣2+5的结果是（ ）A、﹣3 B、-2 C、+2 D、32. 如图是由相同小正方体组成的立体图形，它的左视图为（ ）
A、
B、
C、
D、
3. 下列计算结果是x5的为（ ）A、x10÷x2 B、x6﹣x C、x2•x3 D、（x3）24. 北京故宫的占地面积约为720 000m2 ， 将720 000用科学记数法表示为（ ）.A、72×104 B、7.2×105 C、7.2×106 D、0.72×1065. 如图，一个圆形转盘被平均分成6个全等的扇形，任意旋转这个转盘1次，则当转盘停止转动时，指针指向阴影部分的概率是（ ）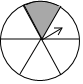
A、 B、 C、 D、6. 若点A（﹣4，y1）、B（﹣2，y2）、C（2，y3）都在反比例函数y＝﹣ 的图象上，则y1、y2、y3的大小关系是（ ）A、y1＞y2＞y3 B、y3＞y2＞y1 C、y2＞y1＞y3 D、y1＞y3＞y27. 如图，已知圆O的半径为10，AB⊥CD，垂足为P，且AB＝CD＝16，则OP的长为（ ）
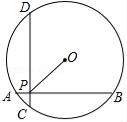A、6 B、6 C、8 D、88. 把一副三角板如图甲放置，其中∠ACB＝∠DEC＝90°，∠A＝45°，∠D＝30°，斜边AB＝6，DC＝7，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长为（ ）
A、 B、5 C、4 D、9. 如图为矩形ABCD，一条直线将该矩形分割成两个多边形，若这两个多边形的内角和分别为a和b，则a+b不可能是（ ）
A、360° B、540° C、630° D、720°10. 二次函数y=﹣x2+mx的图象如图，对称轴为直线x=2，若关于x的一元二次方程﹣x2+mx﹣t=0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是（ ）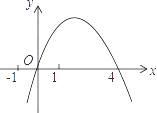
A、t＞﹣5 B、﹣5＜t＜3 C、3＜t≤4 D、﹣5＜t≤4二、填空题：共6小题，每小题5分，共30分.
-
11. 因式分解：2x2﹣4x═ ．12. 如图，AB∥CD，E是BC延长线上一点，若∠B=50°，∠D=20°，则∠E的度数为.
13. 如图，数轴上A、B两点所表示的数分别是﹣4和2，点C是线段AB的中点，则点C所表示的数是.
14. 如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是.(结果保留 )
15. 如图，在矩形ABCD中，AB＝12，BC＝16，点E是BC中点，点F是边CD上的任意一点，当△AEF的周长最小时，则DF的长为
16. 图1是甲、乙两个圆柱形水槽，一个圆柱形的空玻璃杯放置在乙槽中（空玻璃杯的厚度忽略不计）.将甲槽的水匀速注入乙槽的空玻璃杯中，甲水槽内最高水位y（厘米）与注水时间t（分钟）之间的函数关系如图2线段DE所示，乙水槽（包括空玻璃杯）内最高水位y（厘米）与注水时间t（分钟）之间的函数关系如图2折线O﹣A﹣B﹣C所示.记甲槽底面积为S1 ， 乙槽底面积为S2 ， 乙槽中玻璃杯底面积为S3 ， 则S1：S2：S3的值为.
三、解答题：本题共8小题，第17-20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分.
-
17. 计算：4sin60°﹣|﹣1|+（ ﹣1）0+18. 先化简 ，然后从﹣1，0，2中选一个合适的x的值，代入求值。19.
如图，信号塔PQ座落在坡度i=1：2的山坡上，其正前方直立着一警示牌．当太阳光线与水平线成60°角时，测得信号塔PQ落在斜坡上的影子QN长为2 米，落在警示牌上的影子MN长为3米，求信号塔PQ的高．（结果不取近似值）
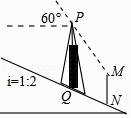20. 在读书月活动中，学校准备购买一批课外读物，为使课外读物满足同学们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息，解答下列问题：
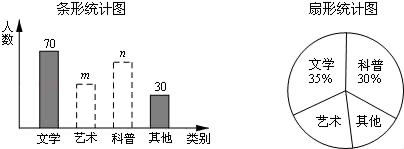(1)、本次调查中，一共调查了名同学；(2)、条形统计图中，m＝ ， n＝；(3)、扇形统计图中，艺术类读物所在扇形的圆心角是度；(4)、学校计划购买课外读物5000册，请根据样本数据，估计学校购买其他类读物多少册比较合理？21. 如图，BD是△ABC的角平分线，它的垂直平分线分别交AB、BC于点E、F、G，连接ED、DG．
(1)、请判断四边形EBGD的形状，并说明理由；(2)、若∠ABC＝30°，∠C＝45°，ED＝2，求GC的长．22. 某工厂为贯彻落实“绿水青山就是金山银山“的发展理念，投资组建了日废水处理量为m吨的废水处理车间，对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大，该车间经常无法完成当天工业废水的处理任务，需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水，每天需固定成本30元，并且每处理一吨废水还需其他费用8元；将废水交给第三方企业处理，每吨需支付12元.根据记录，5月21日，该厂产生工业废水35吨，共花费废水处理费370元.(1)、求该车间的日废水处理量m；(2)、为实现可持续发展，走绿色发展之路，工厂合理控制了生产规模，使得每天废水处理的平均费用不超过10元/吨，试计算该厂一天产生的工业废水量的范围.23. 如图，四边形ABCD内接于⊙O，AB＝AC，AC⊥BD，垂足为E，点F在BD的延长线上，且DF＝DC，连接AF、CF.
(1)、求证：∠BAC＝2∠CAD；(2)、若AF＝10，BC＝4 ，求tan∠BAD的值.24. 如图，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣2，0）和B（l，0），与y轴交于点C.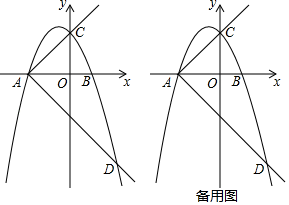
(1)、求抛物线的表达式；(2)、作射线AC，将射线AC绕点A顺时针旋转90°交抛物线于另一点D，在射线AD上是否存在一点H，使△CHB的周长最小.若存在，求出点H的坐标；若不存在，请说明理由；(3)、在（2）的条件下，点Q为抛物线的顶点，点P为射线AD上的一个动点，且点P的横坐标为t，过点P作x轴的垂线l，垂足为E，点P从点A出发沿AD方向运动，直线l随之运动，当﹣2＜t＜1时，直线l将四边形ABCQ分割成左右两部分，设在直线l左侧部分的面积为S，求S关于t的函数表达式.