江苏省淮安市清江浦区2020年九年级质量调研数学试卷(1)
试卷更新日期:2020-05-26 类型:中考模拟
一、选择题
-
1. 2的相反数是( )A、 B、-2 C、 D、2. 要使二次根式 有意义,则 的取值范围是 ( )
A、 B、 C、 D、3. 4月24日是中国航天日.1970年的这一天,我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射,标志着中国从此进入了太空时代,它的运行轨道,距地球最近点439000米,将439000用科学记数法表示应为( )A、0.439×106 B、4.39×106 C、4.39×105 D、439×1034. 如图,由 个相同正方体组合而成的几何体,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列计算正确的是( )A、 B、 C、 D、6. 抽样调查了某校30位女生所穿鞋子的尺码,数据如下(单位:码)
5. 下列计算正确的是( )A、 B、 C、 D、6. 抽样调查了某校30位女生所穿鞋子的尺码,数据如下(单位:码)码号
33
34
35
36
37
人数
7
6
15
1
1
这组数据的中位数和众数分别是( )
A、35,35 B、35,37 C、15,15 D、15,357. 如图,在菱形ABCD中,对角线AC,BD相交于点 ,则BD的长为( ) A、 B、 C、 D、8. 如图,已知A为反比例函数 的图像上一点,过点A作 轴,垂足为B.若 的面积为1,则k的值为( )
A、 B、 C、 D、8. 如图,已知A为反比例函数 的图像上一点,过点A作 轴,垂足为B.若 的面积为1,则k的值为( )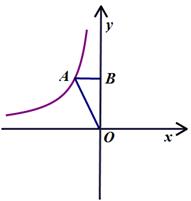 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 分解因式: .10. 若分式 的值为0,则X的值为.11. 如图,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为.
 12. 圆锥底面圆的半径为2,母线长为5,它的侧面积等于(结果保留π).13. 如图,点A,B,C在 上, ,则 的度数是.
12. 圆锥底面圆的半径为2,母线长为5,它的侧面积等于(结果保留π).13. 如图,点A,B,C在 上, ,则 的度数是. 14. 在平面直角坐标系中,将点(3,﹣2)先向右平移2个单位长度,再向上平移3个单位长度,则所得点的坐标是.15. 有4根细木棒,长度分别为2cm、3cm、4cm、5cm,从中任选3根,恰好能搭成一个三角形的概率是 .16. 如图,正方形ABCD的边长为2,E为BC上一点,且 F为AB边上的一个动点,连接EF,以EF为底向右侧作等腰直角 ,连接CG,则CG的最小值为.
14. 在平面直角坐标系中,将点(3,﹣2)先向右平移2个单位长度,再向上平移3个单位长度,则所得点的坐标是.15. 有4根细木棒,长度分别为2cm、3cm、4cm、5cm,从中任选3根,恰好能搭成一个三角形的概率是 .16. 如图,正方形ABCD的边长为2,E为BC上一点,且 F为AB边上的一个动点,连接EF,以EF为底向右侧作等腰直角 ,连接CG,则CG的最小值为.
三、解答题
-
17.(1)、计算:(2)、解不等式:18. 先化简、再求值: ,其中 .19. 如图,在矩形ABCD中,点E,F在对角线BD上,BE=DF请你判断: AE与CF的关系,并加以证明,(友情提示: 不要漏解! )
 20. 央视热播节目“朗读者”激发了学生的阅读兴趣,某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题
20. 央视热播节目“朗读者”激发了学生的阅读兴趣,某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题
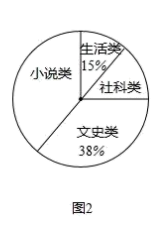 (1)、此次共调查了名学生;(2)、将条形统计图1补充完整;(3)、图2中“社科类”所在扇形的圆心角为 度;(4)、若该校共有学生 人,估计该校喜欢“社科类”书籍的学生人数.21. 小明在上学的路上要经过多个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.如果有2个路口,求小明在上学路上到第二个路口时第一次遇到红灯的概率.(请用“画树状图”或“列表”等方法写出分析过程)22. 学校计划为疫情期间表现优秀的学生购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元(1)、求A,B两种奖品的单价;(2)、学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的一半,请设计出最省钱的购买方案,并说明理由.23. 为加快城乡对接,建设全域美丽乡村,某地区对A,B两地间的公路进行改建.如图,A,B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米, . (结果精确到 千米,参考数据: )
(1)、此次共调查了名学生;(2)、将条形统计图1补充完整;(3)、图2中“社科类”所在扇形的圆心角为 度;(4)、若该校共有学生 人,估计该校喜欢“社科类”书籍的学生人数.21. 小明在上学的路上要经过多个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到信号灯是相互独立的.如果有2个路口,求小明在上学路上到第二个路口时第一次遇到红灯的概率.(请用“画树状图”或“列表”等方法写出分析过程)22. 学校计划为疫情期间表现优秀的学生购买奖品.已知购买3个A奖品和2个B奖品共需120元;购买5个A奖品和4个B奖品共需210元(1)、求A,B两种奖品的单价;(2)、学校准备购买A,B两种奖品共30个,且A奖品的数量不少于B奖品数量的一半,请设计出最省钱的购买方案,并说明理由.23. 为加快城乡对接,建设全域美丽乡村,某地区对A,B两地间的公路进行改建.如图,A,B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米, . (结果精确到 千米,参考数据: )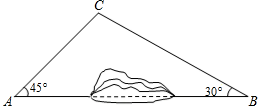 (1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?24. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为)(km),图中的折线表示y与x之间的函数关系,根据图象进行探究:
(1)、开通隧道前,汽车从A地到B地大约要走多少千米?(2)、开通隧道后,汽车从A地到B地大约可以少走多少千米?24. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为)(km),图中的折线表示y与x之间的函数关系,根据图象进行探究: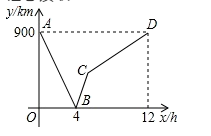 (1)、甲、乙两地之间的距离为 ;(2)、请解释图中点B的实际意义:;(3)、求线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围.25. 如图,四边形ABCD内接于 为 的直径,D为弧AC的中点,过点D作 ,交BC的延长线于点E.
(1)、甲、乙两地之间的距离为 ;(2)、请解释图中点B的实际意义:;(3)、求线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围.25. 如图,四边形ABCD内接于 为 的直径,D为弧AC的中点,过点D作 ,交BC的延长线于点E. (1)、判断DE与 的位置关系,并说明理由;(2)、若 的半径为5,BC=6, 求CE的长.26. 在 中, . 点P是平面内不与点A,C重合的任意一点, 连接AP,将线段AP绕点P逆时针旋转a得到线段DP,连接AD,BD,CP
(1)、判断DE与 的位置关系,并说明理由;(2)、若 的半径为5,BC=6, 求CE的长.26. 在 中, . 点P是平面内不与点A,C重合的任意一点, 连接AP,将线段AP绕点P逆时针旋转a得到线段DP,连接AD,BD,CP
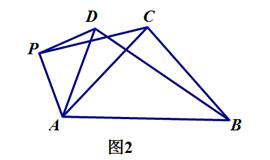 (1)、动手操作
(1)、动手操作如图1,当 时,我们通过用 刻度尺和量角器度量发现:
的值是1;直线BD与直线CP相交所成的较小角的度数是 ;
请证明以上结论正确.
(2)、类比探究如图2,当 时,请写出 的值及直线BD与直线CP相交所成的较小角的度数,并就图2的情形说明理由.
27. 如图,抛物线 经过点两点 ,与V轴交于点C,点D是抛物线上一个动点,设点D的横坐标为 .连接AC、BC、DB、DC. (1)、求抛物线的函数表达式;(2)、当 的面积等于 的面积时,求 的值;(3)、当 时,若点M是x轴正半轴上上的一个动点,点N是抛物线上动点,试判断是否存在这样的点M,使得以点B、D、M、N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标:若不存在,请说明理由.
(1)、求抛物线的函数表达式;(2)、当 的面积等于 的面积时,求 的值;(3)、当 时,若点M是x轴正半轴上上的一个动点,点N是抛物线上动点,试判断是否存在这样的点M,使得以点B、D、M、N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标:若不存在,请说明理由.