江苏省无锡市2020年数学中考模拟试卷(4月)
试卷更新日期:2020-05-26 类型:中考模拟
一、2020年江苏省无锡市中考数学4月模拟试题
-
1. -4的倒数是( )A、 B、 C、 D、2. 下列计算中正确的是( )A、a2+b3=2a5 B、a4÷a=a4 C、a2•a4=a8 D、(﹣a2)3=﹣a63.
抢微信红包成为节日期间人们最喜欢的活动之一.对某单位50名员工在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
 A、20,20 B、30,20 C、30,30 D、20,304. 函数y=﹣2x2先向右平移1个单位,再向下平移2个单位,所得函数解析式是( )A、y=﹣2(x﹣1)2+2 B、y=﹣2(x﹣1)2﹣2 C、y=﹣2(x+1)2+2 D、y=﹣2(x+1)2﹣25. 已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是( )A、8 B、9 C、10 D、126. 下列图形为正多边形的是( )A、
A、20,20 B、30,20 C、30,30 D、20,304. 函数y=﹣2x2先向右平移1个单位,再向下平移2个单位,所得函数解析式是( )A、y=﹣2(x﹣1)2+2 B、y=﹣2(x﹣1)2﹣2 C、y=﹣2(x+1)2+2 D、y=﹣2(x+1)2﹣25. 已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是( )A、8 B、9 C、10 D、126. 下列图形为正多边形的是( )A、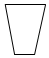 B、
B、 C、
C、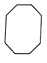 D、
D、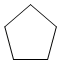 7. 用一个半径为15、圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是( )A、5 B、10 C、5π D、10π8. 如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为( )
7. 用一个半径为15、圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是( )A、5 B、10 C、5π D、10π8. 如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为( )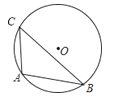 A、1 B、2 C、2 D、9. 如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,过点F作AD的平行线分别交DC、AB于点M、N,则S△BNF:S△DMF等于( )
A、1 B、2 C、2 D、9. 如图,在▱ABCD中,点E是边AD的中点,EC交对角线BD于点F,过点F作AD的平行线分别交DC、AB于点M、N,则S△BNF:S△DMF等于( ) A、9:4 B、4:1 C、3:1 D、2:110. 在平面直角坐标系中,已知 中的直角顶点C落在第一象限, , ,且BC=6,则C点的坐标是( )A、 B、 C、 D、11. 计算 .12. 分解因式6xy2-9x2y-y3 = .13. 某公益机构设立了网站接受爱心捐助,旨在推动社会和谐,发展公益慈善事业,据网站统计,目前已有大约2451000人献爱心,将“2451000”用科学记数法表示是.14. 如图,已知A( ,y1),B(2,y2)为反比例函数y= 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是.
A、9:4 B、4:1 C、3:1 D、2:110. 在平面直角坐标系中,已知 中的直角顶点C落在第一象限, , ,且BC=6,则C点的坐标是( )A、 B、 C、 D、11. 计算 .12. 分解因式6xy2-9x2y-y3 = .13. 某公益机构设立了网站接受爱心捐助,旨在推动社会和谐,发展公益慈善事业,据网站统计,目前已有大约2451000人献爱心,将“2451000”用科学记数法表示是.14. 如图,已知A( ,y1),B(2,y2)为反比例函数y= 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是.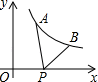 15. 甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:S甲2=2,S乙2=4,则射击成绩较稳定的是(选填“甲”或“乙”).16. 如图,把△ABC绕着点A顺时针方向旋转角度α(0°<α<90°),得到△AB'C',若B',C,C'三点在同一条直线上,∠B'CB=46°,则α的度数是.
15. 甲、乙两人各进行10次射击比赛,平均成绩均为9环,方差分别是:S甲2=2,S乙2=4,则射击成绩较稳定的是(选填“甲”或“乙”).16. 如图,把△ABC绕着点A顺时针方向旋转角度α(0°<α<90°),得到△AB'C',若B',C,C'三点在同一条直线上,∠B'CB=46°,则α的度数是.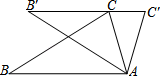 17. 如图,在菱形ABCD中,连接BD,点E在AB上,连接CE交BD于点F,作FG⊥BC于点G,∠BEC=3∠BCE,BF= DF,若FG= ,则AB的长为.
17. 如图,在菱形ABCD中,连接BD,点E在AB上,连接CE交BD于点F,作FG⊥BC于点G,∠BEC=3∠BCE,BF= DF,若FG= ,则AB的长为.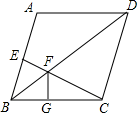 18. 若关于x的一元二次方程ax2+2x-5=0的两根中有且仅有一根在0与1之间(不含0和1),则a的取值范围是.19.(1)、计算: +2×(﹣5)+(﹣3)2+20140;(2)、化简:(a+1)2+2(1﹣a).20. 计算题(1)、解方程组: .(2)、解不等式组: ,并写出它的所有正整数解.21. 如图,点A、B、C、D在同一条直线上,CE∥DF,EC=BD,AC=FD,求证:AE=FB.
18. 若关于x的一元二次方程ax2+2x-5=0的两根中有且仅有一根在0与1之间(不含0和1),则a的取值范围是.19.(1)、计算: +2×(﹣5)+(﹣3)2+20140;(2)、化简:(a+1)2+2(1﹣a).20. 计算题(1)、解方程组: .(2)、解不等式组: ,并写出它的所有正整数解.21. 如图,点A、B、C、D在同一条直线上,CE∥DF,EC=BD,AC=FD,求证:AE=FB.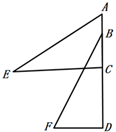 22. 如图,△ABC的三个顶点都在⊙O上,直径AD=6cm , ∠DAC=2∠B , 求AC的长.
22. 如图,△ABC的三个顶点都在⊙O上,直径AD=6cm , ∠DAC=2∠B , 求AC的长.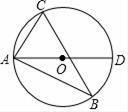 23. 为激发学生的阅读兴趣,培养学生良好的阅读习惯,我区某校欲购进一批学生喜欢的图书,学校组织学生会随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
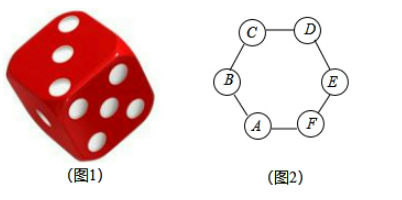
23. 为激发学生的阅读兴趣,培养学生良好的阅读习惯,我区某校欲购进一批学生喜欢的图书,学校组织学生会随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题: (1)、填空或选择:此次共调查了名学生;图2中“小说类”所在扇形的圆心角为度;学生会采用的调查方式是.A.普查 B.抽样调查(2)、将条形统计图(图1)补充完整;(3)、若该校共有学生2500人,试估计该校喜欢“社科类”书籍的学生人数.24. 如图1,骰子有六个面并分别标有数1,2,3,4,5,6,如图2,正六边形ABCDEF顶点处各有一个圈,跳圈游戏的规则为:游戏者掷一次骰子,骰子向上的一面上的数字是几,就沿正六边形的边顺时针方向连续跳几个边长.
(1)、填空或选择:此次共调查了名学生;图2中“小说类”所在扇形的圆心角为度;学生会采用的调查方式是.A.普查 B.抽样调查(2)、将条形统计图(图1)补充完整;(3)、若该校共有学生2500人,试估计该校喜欢“社科类”书籍的学生人数.24. 如图1,骰子有六个面并分别标有数1,2,3,4,5,6,如图2,正六边形ABCDEF顶点处各有一个圈,跳圈游戏的规则为:游戏者掷一次骰子,骰子向上的一面上的数字是几,就沿正六边形的边顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈F;……设游戏者从圈A起跳.
 (1)、小明随机掷一次骰子,求落回到圈A的概率 ;(2)、小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率 ,并指出他与小明落回到圈A的可能性一样吗?25. “壮丽70载,奋进新时代”.值伟大祖国70华诞之际,某网店特别推出甲、乙两种纪念文化衫,已知甲种纪念文化衫的售价比乙种纪念文化衫多15元,广益中学陈老师从该网店购买了2件甲种纪念文化衫和3件乙种纪念文化衫,共花费255元.(1)、该网店甲、乙两种纪念文化衫每件的售价各是多少元?(2)、根据消费者需求,该网店决定用不超过8780元购进甲、乙两种纪念文化衫共200件,且甲种纪念文化衫的数量大于乙种纪念文化衫数量的 ,已知甲种纪念文化衫每件的进价为50元,乙种纪念文化衫每件的进价为40元.
(1)、小明随机掷一次骰子,求落回到圈A的概率 ;(2)、小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率 ,并指出他与小明落回到圈A的可能性一样吗?25. “壮丽70载,奋进新时代”.值伟大祖国70华诞之际,某网店特别推出甲、乙两种纪念文化衫,已知甲种纪念文化衫的售价比乙种纪念文化衫多15元,广益中学陈老师从该网店购买了2件甲种纪念文化衫和3件乙种纪念文化衫,共花费255元.(1)、该网店甲、乙两种纪念文化衫每件的售价各是多少元?(2)、根据消费者需求,该网店决定用不超过8780元购进甲、乙两种纪念文化衫共200件,且甲种纪念文化衫的数量大于乙种纪念文化衫数量的 ,已知甲种纪念文化衫每件的进价为50元,乙种纪念文化衫每件的进价为40元.①若设购进甲种纪念文化衫m件,则该网店有哪几种进货方案?
②若所购进纪念文化衫均可全部售出,请求出网店所获利润W(元)与甲种纪念文化衫进货量m(件)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
26. 如图,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C、F在抛物线上,点D、E在x轴上,CF交y轴于点B(0,2),且矩形其面积为8,此抛物线的解析式.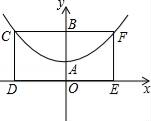 27. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
27. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.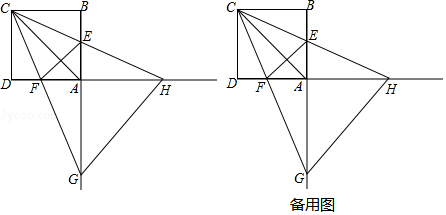 (1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,
(1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
28. 如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数. (1)、判断四边形DEFB的形状.并证明你的结论;(2)、试求四边形DEFB的面积S与b的关系式;(3)、设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.
(1)、判断四边形DEFB的形状.并证明你的结论;(2)、试求四边形DEFB的面积S与b的关系式;(3)、设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.