江苏省苏北地区2020年数学中考模拟试卷（3月）

试卷更新日期：2020-05-26 类型：中考模拟

进入出卷网下载

一、选择题

1. －5的相反数是（）

A、-5 B、5 C、 $\frac{1}{5}$ D、 $- \frac{1}{5}$

查看试题解析
2. 下列运算正确的是（）

A、2a+3b＝5ab B、（a+b）²＝a²+b² C、a²•a³＝a⁶ D、5a﹣2a＝3a

查看试题解析
3. 0.000182用科学记数法表示应为（）

A、0182×10^﹣³ B、1.82×10^﹣⁴ C、1.82×10^﹣⁵ D、18.2×10^﹣⁴

查看试题解析
4. 已知a＞b，则下列式子中错误的是（）

A、a+2＞b+2 B、4a＞4b C、﹣a＞﹣b D、4a﹣3＞4b﹣3

查看试题解析
5.
在平面直角坐标系中，一次函数y=kx+b的图象如图所示，观察图象可得（）

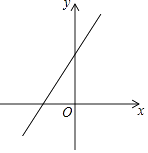A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
6. 如图，直线a，b被直线c所截，a∥b，若∠2＝45°，则∠1等于（）

A、125° B、130° C、135° D、145°

查看试题解析
7. 下列长度的三条线段，能组成三角形的是（）

A、4cm，5cm，9cm B、8cm，8cm，15cm C、5cm，5cm，10cm D、6cm，7cm，14cm

查看试题解析
8. 若函数 $y = x^{2} - 2 x + b$ 的图象与坐标轴有三个交点，则 $b$ 的取值范围是（）

A、 $b < 1 且 b \neq 0$ B、 $b > 1$ C、 $0 < b < 1$ D、 $b < 1$

查看试题解析

二、填空题

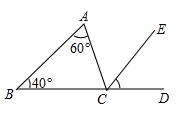
9. 分解因式：3x²-6x+3= ．

查看试题解析
10. 若关于x、y的二元一次方程3x﹣ay=1有一个解是 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ ，则a=.

查看试题解析
11. 已知B是线段AD上一点，C是线段AD的中点，若AD＝10，BC＝3，则AB＝.

查看试题解析
12. 如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A= $60 °$ ，∠B= $40 °$ ，则∠ECD等于.

查看试题解析
13. 点P(2，-5)关于x轴对称的点的坐标为

查看试题解析
14. 已知反比例函数y＝ $\frac{n + 3}{x}$ 的图象，在同一象限内，y随x的增大而增大，则n的取值范围是.

查看试题解析
15. 如图，下列图案由边长均等的黑、白两色正方形按一定规律拼接而成，按此规律，第n个图案中白色正方形的个数为个.

查看试题解析

三、解答题

16.

(1)、计算：﹣1²+2020⁰﹣ ${(\frac{1}{2})}^{- 1}$ + $\sqrt[3]{8}$ ；

(2)、化简 $\frac{x - 2}{x^{2}} \div (1 - \frac{2}{x})$

查看试题解析
17. 解方程：

(1)、 $\frac{x + 1}{2} - 1 = \frac{2 - 3 x}{3}$ ；

(2)、2x²﹣x﹣1＝0

查看试题解析
18.

(1)、解方程： $\frac{x + 1}{x - 1} - \frac{4}{x^{2} - 1} = 1$ .

(2)、解不等式组 ${\begin{array}{l} 2 x \geq - 9 - x \\ 5 x - 1 > 3 (x + 1) \end{array}$ ，并把它的解集在数轴上表示出来.

查看试题解析
19. 如图，△ABC中，AB=AC，点E，F在边BC上，BE=CF，点D在AF的延长线上，AD=AC．

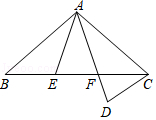(1)、求证：△ABE≌△ACF；

(2)、若∠BAE=30°，则∠ADC=°．

查看试题解析
20. 小丽购买学习用品的收据如表，因污损导致部分数据无法识别，根据下表，解决下列问题：

(1)、小丽买了自动铅笔、记号笔各几支？

(2)、若小丽再次购买软皮笔记本和自动铅笔两种文具，共花费15元，则有哪几种不同的购买方案？
商品名
单价（元）
数量（个）
金额（元）
签字笔
3
2
6
自动铅笔
1.5
●
●
记号笔
4
●
●
软皮笔记本
●
2
9
圆规
3.5
1
●
合计

8
28

查看试题解析
21. 学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地.两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示.

(1)、根据图象信息，当t＝分钟时甲乙两人相遇，甲的速度为米/分钟，乙的速度为米/分钟；

(2)、图中点A的坐标为；

(3)、求线段AB所直线的函数表达式；

(4)、在整个过程中，何时两人相距400米？

查看试题解析
22. 已知一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x}$ 的图象交于点 $A$ ，与 $x$ 轴交于点 $B (5 ， 0)$ ，若 $O B = A B$ ，且 $S_{Δ O A B} = \frac{15}{2}$ .

(1)、求反比例函数与一次函数的表达式；

(2)、若点 $P$ 为x轴上一点， $Δ A B P$ 是等腰三角形，求点 $P$ 的坐标.

查看试题解析
23. 如图所示，二次函数y＝k（x﹣1）²+2的图象与一次函数y＝kx﹣k+2的图象交于A、B两点，点B在点A的右侧，直线AB分别与x、y轴交于C、D两点，其中k＜0.

(1)、求A、B两点的横坐标；

(2)、若△OAB是以OA为腰的等腰三角形，求k的值；

(3)、二次函数图象的对称轴与x轴交于点E，是否存在实数k，使得∠ODC＝2∠BEC，若存在，求出k的值；若不存在，说明理由.

查看试题解析

商品名	单价（元）	数量（个）	金额（元）
签字笔	3	2	6
自动铅笔	1.5	●	●
记号笔	4	●	●
软皮笔记本	●	2	9
圆规	3.5	1	●
合计		8	28