江苏省淮安市2020年数学中考全真模拟试卷

试卷更新日期：2020-05-26 类型：中考模拟

进入出卷网下载

一、选择题

1. 若y=（m＋1） $x^{m^{2} - 6 m - 5}$ 是二次函数，则m=（）

A、－1 B、7 C、－1或7 D、以上都不对

查看试题解析
2. 若 $\frac{b}{a - b}$ = $\frac{1}{4}$ ，则 $\frac{a}{b}$ 的值为（）

A、5 B、 $\frac{1}{5}$ C、3 D、 $\frac{1}{3}$

查看试题解析
3. 下列四条线段能成比例线段的是（）

A、1，1，2，3 B、1，2，3，4 C、2，2，3，3 D、2，3，4，5

查看试题解析
4. 如图所示，若△ABC∽△DEF，则∠E的度数为（）

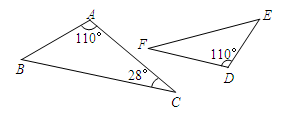A、28° B、32° C、42° D、52°

查看试题解析
5. 如图，△ABC与△DEF都是等腰三角形，且AB=AC=3，DE=DF=2，若∠B+∠E=90°，则△ABC与△DEF的面积比为（　　）

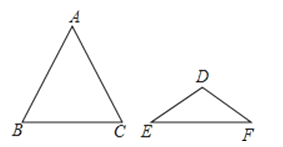A、9：4 B、3：2 C、 $\sqrt{3}$ ： $\sqrt{2}$ D、3 $\sqrt{3}$ ：2 $\sqrt{2}$

查看试题解析
6. 一个不透明的盒子中装有6个大小相同的乒乓球，其中4个是黄球，2个是白球.从该盒子中任意摸出一个球，摸到黄球的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{2}{5}$

查看试题解析
7. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，BC=3，AC=4，tan∠BCD的值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{4}{5}$ D、 $\frac{5}{4}$

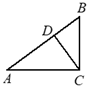查看试题解析
8. 已知：如图，Rt△ABC中，∠BAC=90°，D是AC上一点，∠ABD=∠C，直线EF过点D，与BA的延长线相交于F，且EF⊥BC，垂足为E.则图中所有与△ABD相似的三角形有多少个（）

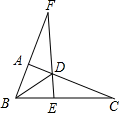A、3 B、4 C、5 D、6

查看试题解析

二、填空题

9. 一个四边形的边长分别是3，4，5，6，另一个与它相似的四边形最小边长为6，则另一个四边形的最长边是.

查看试题解析
10. 若二次函数y＝2（x+1）²+3的图象上有三个不同的点A（x₁ ， 4）、B（x₁+x₂ ， n）、C（x₂ ， 4），则n的值为.

查看试题解析
11. 在Rt△ABC中，∠C=90°，若tanA= $\frac{2}{5}$ ，则tanB=.

查看试题解析
12. 联结三角形各边中点，所得的三角形的周长与原三角形周长的比是.

查看试题解析
13. 在平面直角坐标系中，将抛物线y=x²+2x+3绕着原点旋转180°，所得抛物线的解析式是.

查看试题解析
14. 在 $Δ ABC$ 中，若 $| s i n A - \frac{1}{2} | + {(t a n B - \frac{\sqrt{3}}{3})}^{2} = 0$ ，则 $Δ ABC$ 是三角形.

查看试题解析
15. 如果点P是线段AB的如黄金分割点，且 $AP > BP$ ， $AP = 2 \sqrt{5} - 2$ ，则 $AB =$ .

查看试题解析
16. 抛物线y=9x²﹣px+4与x轴只有一个公共点，则p的值是.

查看试题解析

三、解答题

17. 计算： ${(π - 3)}^{0} - 2 \sqrt{3} \sin 60 ° - {(\frac{1}{3})}^{- 2}$

查看试题解析
18. 如图，在Rt△ABC中，∠ACB=90º，AC=2，BC=3．点D为AC的中点，联结BD ，过点C作CG⊥BD ，交AC的垂线AG于点G ， GC分别交BA、BD于点F、E ．

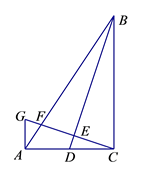(1)、求GA的长；

(2)、求△AFC的面积．

查看试题解析
19. 在A市建设规划图上，城区南北长为240cm，A市城区南北的实际长为18km，试写出该规划图的比例尺.

查看试题解析
20. 计算：2cos²45°+tan60°•tan30°﹣cos60°

查看试题解析
21. 已知二次函数的顶点坐标为 $(2 ， - 2)$ ，且其图象经过点 $(1 ， - 1)$ ，求此二次函数的解析式.

查看试题解析
22. 如图示，在 $Δ ABC$ 中， $A C = 8$ ， $∠ A = 30 °$ ， $∠ B = 45 °$ ，求 $Δ ABC$ 的面积.

查看试题解析
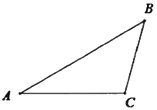23. 小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=﹣10x+500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．

(1)、设小明每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．

(2)、当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？

(3)、如果小明想要每月获得的利润不低于2000元，那么小明每月的成本最少需要多少元？（成本=进价×销售量）

查看试题解析
24. 如图所示，在等腰△ABC中，AB＝AC＝10cm，BC＝16cm．点D由点A出发沿AB方向向点B匀速运动，同时点E由点B出发沿BC方向向点C匀速运动，它们的速度均为1cm/s．连接DE，设运动时间为t（s）（0＜t＜10），解答下列问题：

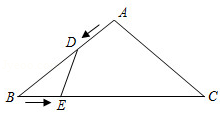(1)、当t为何值时，△BDE的面积为7.5cm²；

(2)、在点D，E的运动中，是否存在时间t，使得
△BDE与△ABC相似？若存在，请求出对应的时间t；若不存在，请说明理由．

查看试题解析
25. 如图，热气球探测器显示，从热气球A处看一栋楼顶部B处的仰角为30°，看这栋楼底部C处的俯角为60°，热气球与楼的水平距离AD为100米，试求这栋楼的高度BC.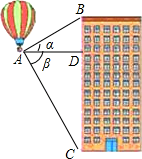

查看试题解析
26. 如图，灯杆AB与墙MN的距离为18米，小丽在离灯杆（底部）9米的D处测得其影长DF为3m，设小丽身高为1.6m.

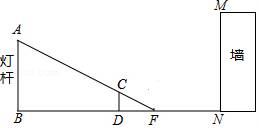(1)、求灯杆AB的高度；

(2)、小丽再向墙走7米，她的影子能否完全落在地面上？若能，求此时的影长；若不能，求落在墙上的影长.

查看试题解析
27. 在Rt△ABC中，∠C＝90°，AC＝20cm，BC＝15cm.现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB也向点B方向运动.如果点P的速度是4cm/秒，点Q的速度是2cm/秒，它们同时出发，当有一点到达所在线段的端点时，就停止运动，设运动的时间为t秒.

(1)、用含t的代数式表示Rt△CPQ的面积S；

(2)、当t＝3秒时，P、Q两点之间的距离是多少？

(3)、当t为多少秒时，以点C、P、Q为顶点的三角形与△ABC相似？

查看试题解析