河南省2020年数学中考二模试卷
试卷更新日期:2020-05-26 类型:中考模拟
一、选择题
-
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期,-2020的相反数是( )A、2020 B、-2020 C、 D、2. 据介绍,2019年央视春晚直播期间,全球观众参与百度APP红包互动活动次数达208亿次.“208亿”用科学记数法表示为( )A、2.08×1010 B、0.208×1011 C、208×108 D、2.08×10113. 如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,FG平分∠EFD交AB于点G,若∠BEF=70°,则∠AGF的度数为( )
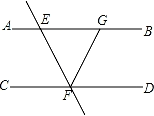 A、35° B、45° C、55° D、65°4. 下列运算正确的是( )A、a2•a2=2a2 B、a2+a2=a4 C、(1+2a)2=1+2a+4a2 D、(﹣a+1)(a+1)=1﹣a25. 如图是某兴趣社制作的模型,则它的俯视图是( )
A、35° B、45° C、55° D、65°4. 下列运算正确的是( )A、a2•a2=2a2 B、a2+a2=a4 C、(1+2a)2=1+2a+4a2 D、(﹣a+1)(a+1)=1﹣a25. 如图是某兴趣社制作的模型,则它的俯视图是( )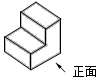 A、
A、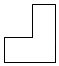 B、
B、 C、
C、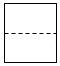 D、
D、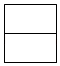 6. 我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长( )尺.A、25 B、20 C、15 D、107. 甲、乙、丙、丁四人进行射箭测试,每人10次,测试成绩的平均数都是8.9环,方差分别是s甲2=0.45,s乙2=0.50,s丙2=0.55,s丁2=0.65,则测试成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁8. 已知关于x的一元二次方程x2﹣m=2x有两个不相等的实数根,则m的取值范围是( )A、m>0 B、m>﹣1 C、m<0 D、m<﹣19. 如图,在正方形网格中用没有刻度的直尺作一组对边长度为 的平行四边形.在1×3的正方形网格中最多作2个,在1×4的正方形网格中最多作6个,在1×5的正方形网格中最多作12个,则在1×8的正方形网格中最多可以作( )
6. 我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果一托为5尺,那么索长( )尺.A、25 B、20 C、15 D、107. 甲、乙、丙、丁四人进行射箭测试,每人10次,测试成绩的平均数都是8.9环,方差分别是s甲2=0.45,s乙2=0.50,s丙2=0.55,s丁2=0.65,则测试成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁8. 已知关于x的一元二次方程x2﹣m=2x有两个不相等的实数根,则m的取值范围是( )A、m>0 B、m>﹣1 C、m<0 D、m<﹣19. 如图,在正方形网格中用没有刻度的直尺作一组对边长度为 的平行四边形.在1×3的正方形网格中最多作2个,在1×4的正方形网格中最多作6个,在1×5的正方形网格中最多作12个,则在1×8的正方形网格中最多可以作( ) A、28个 B、42个 C、21个 D、56个10. 如图1,在△ABC中,AB=AC,BC=m,D,E分别是AB,AC边的中点,点P为BC边上的一个动点,连接PD,PA,PE.设PC=x,图1中某条线段长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线可能是( )
A、28个 B、42个 C、21个 D、56个10. 如图1,在△ABC中,AB=AC,BC=m,D,E分别是AB,AC边的中点,点P为BC边上的一个动点,连接PD,PA,PE.设PC=x,图1中某条线段长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线可能是( )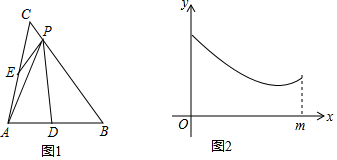 A、PB B、PE C、PA D、PD
A、PB B、PE C、PA D、PD二、填空题
-
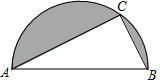
11. 计算: .12. 不等式组 的解集为.13. 把反面完全相同,正面分别写着“全”“能”“模”“考”的4张卡片洗匀后反面朝上放在桌面上,从中随机抽取两张,则抽出的卡片上的汉字恰好组成“模考”的概率是.14. 已知点C在以AB为直径的半圆上,连结AC、BC,AB=10,BC:AC=3:4,阴影部分的面积为.
 15. 如图所示,矩形ABCD中,AB=5,BC=8,点P为BC上一动点(不与端点重合),连接AP,将△ABP沿着AP折叠.点B落到M处,连接BM、CM,若△BMC为等腰三角形,则BP的长度为.
15. 如图所示,矩形ABCD中,AB=5,BC=8,点P为BC上一动点(不与端点重合),连接AP,将△ABP沿着AP折叠.点B落到M处,连接BM、CM,若△BMC为等腰三角形,则BP的长度为.
三、解答题
-
16. 先化简,再求值:(2﹣ )÷ ,其中x= ﹣3.17. 如图,AB是☉ 的直径, 为☉ 上一点,P是半径OB上一动点(不与O,B重合),过点[作射线 ,分别交弦BC, 于D,E两点,过点C的切线交射线l于点F.
 (1)、求证: .(2)、当E是 的中点时,
(1)、求证: .(2)、当E是 的中点时,①若 ,判断以O,B,E,C为顶点的四边形是什么特殊四边形,并说明理由;
②若 ,且AB=30,则OP=▲。
18. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校响应号召,鼓励师生利用课余时间广泛阅读,该校文学社为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:一 数据收集,从全校随机抽取20学生,进行每周用于课外阅读时间的调查,数据如下(单位: ):
30
60
81
50
44
110
130
146
80
100
60
80
120
140
75
81
10
30
81
92
二 整理数据,按如下分段整理样本数据并补全表格:
课外阅读时间
等级
人数
3
8
三 分析数据,补全下列表格中的统计量:
平均数
中位数
众数
80
81
四 得出结论:
①表格中的数据: , , ;
②用样本中的统计量估计该校学生每周用于课外阅读时间的等级为;
③如果该校现有学生400人,估计等级为“ ”的学生有人;
④假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)
平均阅读本课外书.
19. 数学活动课上,小明和小红要测量小河对岸大树BC的高度,小红在点A测得大树顶端B的仰角为45°,小明从A点出发沿斜坡走3 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.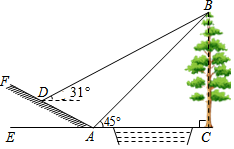 (1)、求小明从点A到点D的过程中,他上升的高度;(2)、依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)20. 甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.
(1)、求小明从点A到点D的过程中,他上升的高度;(2)、依据他们测量的数据能否求出大树BC的高度?若能,请计算;若不能,请说明理由.(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)20. 甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示. (1)、求甲、乙两车行驶的速度V甲、V乙.(2)、求m的值.(3)、若甲车没有故障停车,求可以提前多长时间两车相遇.21. 如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)、求甲、乙两车行驶的速度V甲、V乙.(2)、求m的值.(3)、若甲车没有故障停车,求可以提前多长时间两车相遇.21. 如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C. (1)、求抛物线的解析式;(2)、点P是抛物线上的动点,且满足S△PAO=2S△PCO , 求出P点的坐标;(3)、连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.22. 等腰直角三角形OAB中,∠OAB=90°,OA=AB,点D为OA中点,DC⊥OB,垂足为C,连接BD,点M为线段BD中点,连接AM、CM,如图①.
(1)、求抛物线的解析式;(2)、点P是抛物线上的动点,且满足S△PAO=2S△PCO , 求出P点的坐标;(3)、连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.22. 等腰直角三角形OAB中,∠OAB=90°,OA=AB,点D为OA中点,DC⊥OB,垂足为C,连接BD,点M为线段BD中点,连接AM、CM,如图①. (1)、求证:AM=CM;(2)、将图①中的△OCD绕点O逆时针旋转90°,连接BD,点M为线段BD中点,连接AM、CM、OM,如图②.
(1)、求证:AM=CM;(2)、将图①中的△OCD绕点O逆时针旋转90°,连接BD,点M为线段BD中点,连接AM、CM、OM,如图②.①求证:AM=CM,AM⊥CM;
②若AB=4,求△AOM的面积.
23. 如图,将抛物线 平移后,新抛物线经过原抛物线的顶点C,新抛物线与x轴正半轴交于点B,联结BC, ,设新抛物线与x轴的另一交点是A,新抛物线的顶点是.D (1)、求点D的坐标;(2)、设点 在新抛物线上,联结AC,DC,如果CE平分 ,求点E的坐标;(3)、在(2)的条件下,将抛物线 沿 轴左右平移,点C的对应点为F,当 和 相似时,请直接写出平移后得到抛物线的表达式.
(1)、求点D的坐标;(2)、设点 在新抛物线上,联结AC,DC,如果CE平分 ,求点E的坐标;(3)、在(2)的条件下,将抛物线 沿 轴左右平移,点C的对应点为F,当 和 相似时,请直接写出平移后得到抛物线的表达式.