河南省2020年大联考数学中考模拟试卷
试卷更新日期:2020-05-26 类型:中考模拟
一、选择题
-
1. ﹣2 的倒数是( )A、2 B、﹣3 C、﹣ D、2. 下列不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 小明将某圆锥形的冰淇淋纸套沿它的一条母线展开 若不考虑接缝,它是一个半径为12cm,圆心角为 的扇形,则A、圆锥形冰淇淋纸套的底面半径为4cm B、圆锥形冰淇淋纸套的底面半径为6cm C、圆锥形冰淇淋纸套的高为 D、圆锥形冰淇淋纸套的高为4. 如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=( )
3. 小明将某圆锥形的冰淇淋纸套沿它的一条母线展开 若不考虑接缝,它是一个半径为12cm,圆心角为 的扇形,则A、圆锥形冰淇淋纸套的底面半径为4cm B、圆锥形冰淇淋纸套的底面半径为6cm C、圆锥形冰淇淋纸套的高为 D、圆锥形冰淇淋纸套的高为4. 如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=( )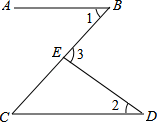 A、65° B、70° C、75° D、80°5. 一元二次方程x2﹣2kx+k2﹣k+2=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣2 B、k<﹣2 C、k<2 D、k>26. 如图,过⊙O上一点C作⊙O的切线,交直径AB的延长线于点D,若∠A=25°,则∠D的度数为( )
A、65° B、70° C、75° D、80°5. 一元二次方程x2﹣2kx+k2﹣k+2=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣2 B、k<﹣2 C、k<2 D、k>26. 如图,过⊙O上一点C作⊙O的切线,交直径AB的延长线于点D,若∠A=25°,则∠D的度数为( ) A、25° B、30° C、40° D、50°7. 已知x1 , x2是方程 的两根,则x12+x22的值为( )A、3 B、5 C、7 D、48. 如图,在矩形ABCD中,AD=5,AB=3,点E时BC上一点,且AE=AD,过点D做DF⊥AE于F,则tan∠CDF的值为( )
A、25° B、30° C、40° D、50°7. 已知x1 , x2是方程 的两根,则x12+x22的值为( )A、3 B、5 C、7 D、48. 如图,在矩形ABCD中,AD=5,AB=3,点E时BC上一点,且AE=AD,过点D做DF⊥AE于F,则tan∠CDF的值为( ) A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,D是AB边上一个动点(不与点A,B重合),E是BC边上一点,且∠CDE=30°.设AD=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,D是AB边上一个动点(不与点A,B重合),E是BC边上一点,且∠CDE=30°.设AD=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、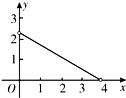 C、
C、 D、
D、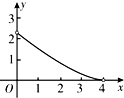 10. 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
10. 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( ) A、3 B、1.5 C、 D、
A、3 B、1.5 C、 D、二、填空题
-
11. 计算: = .12. 十九大报告中指出,过去五年,我国国内生产总值从54万亿元增长到80万亿元,对世界经济增长贡献率超过30%,其中“80万亿元”用科学记数法表示为元.13. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为 .
 14. 如图,已知第一象限内的点A在反比例函数 上,第二象限的点B在反比例函数 上,且OA⊥OB, ,则k的值为 .
14. 如图,已知第一象限内的点A在反比例函数 上,第二象限的点B在反比例函数 上,且OA⊥OB, ,则k的值为 . 15. 矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为.
15. 矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为.
三、解答题
-
16. 先化简,再求值 ,且x是不等式 ≤1的最小整数解.17. 上海世博会已于2010年4月30日开幕,各国游客都被吸引到了这个地方,据统计到5月10号为止最高单日接待量已达到100万人次,其中中国馆自然是最受欢迎的展馆,在世博会开园第一天共接待了游客3万余人,而外国场馆中最受欢迎的依次是瑞士馆、法国馆、德国馆、西班牙馆、日本馆.现将某天世博会最受欢迎的6个馆的参观人数用统计图①②分别表示如下:

请根据统计图回答下列问题:
(1)、这一天参观这6个场馆的总人数为 , 其中参观日本馆的人数有 , 德国馆所在扇形的圆心角度数为;(2)、请将条形统计图补充完整;(3)、小宝和小贝都想利用暑假去上海参观世博会,恰好张伯伯有一张世博会的门票,小宝和小贝都想得到这张门票.于是他们决定用转转盘的游戏来决定这张票由谁获得,游戏规则如下:将一质地均匀的转盘等分成5个面积相等的扇形,上面分别标有数字 -l,4,5,-6,0,小宝和小贝均随机地转转盘一次,把指针指向区域内的数字分别记为x、y.若指针指在边界,则重新转一次直到指针指向一个区域内为止,然后他们计算出xy的值.规定:当xy的值为负数时,门票归小宝;xy的值为正数时,门票归小贝.请利用表格或树状图分析:游戏对双方公平吗?18. 如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF. (1)、当∠BAC=30º时,求△ABC的面积;(2)、当DE=8时,求线段EF的长;(3)、在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.19. 如图,△OA1B1 , △B1A2B2是等边三角形,点A1 , A2在函数 的图象上,点B1 , B2在x轴的正半轴上,分别求△OA1B1 , △B1A2B2的面积.
(1)、当∠BAC=30º时,求△ABC的面积;(2)、当DE=8时,求线段EF的长;(3)、在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.19. 如图,△OA1B1 , △B1A2B2是等边三角形,点A1 , A2在函数 的图象上,点B1 , B2在x轴的正半轴上,分别求△OA1B1 , △B1A2B2的面积.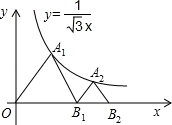 20. 如图所示,在坡角为30°的山坡上有一竖立的旗杆AB,其正前方矗立一墙,当阳光与水平线成45°角时,测得旗杆AB落在坡上的影子BD的长为8米,落在墙上的影子CD的长为6米,求旗杆AB的高(结果保留根号).
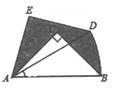
20. 如图所示,在坡角为30°的山坡上有一竖立的旗杆AB,其正前方矗立一墙,当阳光与水平线成45°角时,测得旗杆AB落在坡上的影子BD的长为8米,落在墙上的影子CD的长为6米,求旗杆AB的高(结果保留根号). 21. 某商场第一次购进20件A商品,40件B商品,共用了1980元.脱销后,在进价不变的情况下,第二次购进40件A商品,20件B商品,共用了1560元.商品A的售价为每件30元,商品B的售价为每件60元.(1)、求A,B两种商品每件的进价分别是多少元?(2)、为了满足市场需求,需购进A,B两种商品共1000件,且A种商品的数量不少于B种商品数量的3倍,请你设计进货方案,使这1000件商品售完后,商场获利最大,并求出最大利润.22. 如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E, .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
21. 某商场第一次购进20件A商品,40件B商品,共用了1980元.脱销后,在进价不变的情况下,第二次购进40件A商品,20件B商品,共用了1560元.商品A的售价为每件30元,商品B的售价为每件60元.(1)、求A,B两种商品每件的进价分别是多少元?(2)、为了满足市场需求,需购进A,B两种商品共1000件,且A种商品的数量不少于B种商品数量的3倍,请你设计进货方案,使这1000件商品售完后,商场获利最大,并求出最大利润.22. 如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E, .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
 (1)、求证: ;(2)、若 ,求 .(3)、如图2,在(2)的条件下,连接CF,求 的值.23. 如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移5个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点C,两函数图象分别交于B、D两点.
(1)、求证: ;(2)、若 ,求 .(3)、如图2,在(2)的条件下,连接CF,求 的值.23. 如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移5个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点C,两函数图象分别交于B、D两点. (1)、求函数y=ax2+bx+c的解析式;(2)、如图2,连接AD、CD、BC、AB,判断四边形ABCD的形状,并说明理由.(3)、如图3,连接BD,点M是y轴上的动点,在平面内是否存在一点N,使以B、D、M、N为顶点的四边形为矩形?若存在,请求出N点的坐标;若不存在,请说明理由.
(1)、求函数y=ax2+bx+c的解析式;(2)、如图2,连接AD、CD、BC、AB,判断四边形ABCD的形状,并说明理由.(3)、如图3,连接BD,点M是y轴上的动点,在平面内是否存在一点N,使以B、D、M、N为顶点的四边形为矩形?若存在,请求出N点的坐标;若不存在,请说明理由.