湖北省孝感市云梦县2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2020-05-26 类型:期中考试
一、选择题
-
1. 计算 的结果为( )A、3 B、 C、 D、2. 如图,直线AB, CD ,EF相交于点O, ∠1的邻补角是( )
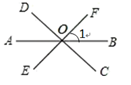 A、∠BOC B、∠BOC和∠AOF C、∠AOF D、∠BOE和∠AOF3. 下列计算正确的是( )A、 B、 C、 D、4. 点P(1,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,下列条件能判定AB∥CD的是( )
A、∠BOC B、∠BOC和∠AOF C、∠AOF D、∠BOE和∠AOF3. 下列计算正确的是( )A、 B、 C、 D、4. 点P(1,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图,下列条件能判定AB∥CD的是( )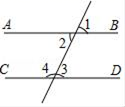 A、∠1=∠2 B、∠1=∠4 C、∠2=∠3 D、∠2+∠3=180°6. 在平面直角坐标系中,把点 先向左平移3个单位长度,再向上平移2个单位长度后得到的点的坐标是( )A、 B、 C、 D、7. 如图, , ,则 ( )
A、∠1=∠2 B、∠1=∠4 C、∠2=∠3 D、∠2+∠3=180°6. 在平面直角坐标系中,把点 先向左平移3个单位长度,再向上平移2个单位长度后得到的点的坐标是( )A、 B、 C、 D、7. 如图, , ,则 ( ) A、 B、 C、 D、8. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间9. 如图,现将一块含有 角的三角板的顶点放在直尺的一边上,若 ,那么 的度数为( )
A、 B、 C、 D、8. 一个正方形的面积是15,估计它的边长大小在( )A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间9. 如图,现将一块含有 角的三角板的顶点放在直尺的一边上,若 ,那么 的度数为( )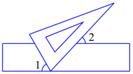 A、 B、 C、 D、10. 下列五个命题:
A、 B、 C、 D、10. 下列五个命题:①如果两个数的绝对值相等,那么这两个数的平方相等;②内错角相等;③在同一平面内,垂直于同一条直线的两条直线互相平行;④两个无理数的和一定是无理数;⑤坐标平面内的点与有序数对是一一对应的.其中真命题的个数是( )
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 的算术平方根是.12. 点M(﹣3,4)到y轴的距离是.13. 已知 ,则 的值为.14. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=80°,则∠BOD=.
 15. 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为.
15. 如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为20cm,则四边形ABFD的周长为.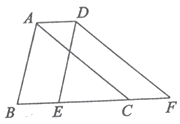 16. 如图,长方形BCDE的各边分别平行于x 轴或y 轴,物体甲和物体乙分别由点 同时出发,沿长方形BCDE 的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是.
16. 如图,长方形BCDE的各边分别平行于x 轴或y 轴,物体甲和物体乙分别由点 同时出发,沿长方形BCDE 的边作环绕运动.物体甲按逆时针方向以2个单位/秒匀速运动,物体乙按顺时针方向以4个单位/秒匀速运动,则两个物体运动后的第2020次相遇地点的坐标是.
三、解答题
-
17. 把下列各数分别填在相应的集合中:
,3.1415926, , , , , , .

 18. 计算.(1)、(2)、19. 如图,两条直线a,b相交.
18. 计算.(1)、(2)、19. 如图,两条直线a,b相交. (1)、如果 ,求 , 的度数;(2)、如果 ,求 , 的度数.20. 已知 的平方根是 , ,求 的立方根.21. 结合图形填空:已知:如图 , .求证: .
(1)、如果 ,求 , 的度数;(2)、如果 ,求 , 的度数.20. 已知 的平方根是 , ,求 的立方根.21. 结合图形填空:已知:如图 , .求证: .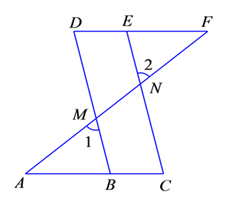
证明:∵ (已知),
又 ( ),
∴ (等量代换),
∴ (同位角相等,两直线平行),
∴ ( ).
∵ (已知),
∴ (等量代换),
∴ ( ),
∴ ( ).