湖北省武汉市东湖高新区2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2020-05-26 类型：期中考试

进入出卷网下载

一、选择题

1. 100的平方根是（）

A、 $\pm 50$ B、50 C、 $\pm 10$ D、10

查看试题解析
2. 在平面直角坐标中，点M（-2，3）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图 $AB / / CD$ 可以得到（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 1 = ∠ 4$ C、 $∠ 2 = ∠ 3$ D、 $∠ 3 = ∠ 4$

查看试题解析
4. 如图，数轴上点A表示的数可能是（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $π$

查看试题解析
5. 下列六个实数：0， $\sqrt{4}$ ， $\sqrt{8}$ ， $\sqrt[3]{8}$ ， $\frac{22}{7}$ ， $\frac{π}{3}$ ，3.14159265，0.10100100010001，0.101001000100001…，其中无理数的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 下列各式中正确的是（）

A、 $\sqrt{36} = \pm 6$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $\sqrt{8} = 4$ D、 ${(\sqrt[3]{- 8})}^{3} = - 8$

查看试题解析
7. 如图，一个含30°角的直角三角板的两个顶点放在一个长方形的对边上，若∠1=20°，那么∠2的度数是（）

A、100° B、105° C、110° D、120°

查看试题解析
8. A地至B地的航线长9360km，一架飞机从A地顺风飞往B地需12h，它逆风飞行同样的航线要13h，则飞机无风时的平均速度是（）

A、720km/h B、750 km/h C、765 km/h D、780 km/h

查看试题解析
9. 下列命题中：①若mn＝0，则点A(m,n)在原点处；②点(2,－m²)一定在第四象限；③已知点A(m,n)与点B(－m,n)，m，n均不为0，则直线AB平行x轴；④已知点A(2,－3)，AB//y轴，且AB=5，则B点的坐标为(2,4)；是真命题的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 若定义：f(a,b)＝(-a,b)，g(m,n)＝(m,-n)，例如f(1,2)＝(-1,2)，g(-4,-5)＝(-4,5)，则g(f(3,-4))的值为（）

A、(3,-4) B、(-3,4) C、(3,4) D、(-3,-4)

查看试题解析

二、填空题

11. 比较两个数的大小： $\sqrt{65}$ 8.（填“＞”、“＜”、“＝”）

查看试题解析
12. 如图，直线AB，CD相交于点O，EO⊥CD，垂足为O.若∠AOE=55°，则∠BOD的度数为.

查看试题解析
13. 已知点P在第四象限，距离x轴4个单位，距离y轴3个单位则点P的坐标为.

查看试题解析
14. 如图，将某动物园中的猴山，狮虎山，熊猫馆分别记为M，N，P，若建立平面直角坐标系，将猴山M，狮虎山N用坐标分别表示为(2，1)和(8，2)，则熊猫馆P用坐标表示为.

查看试题解析
15. 已知等式y＝ax²＋bx＋c，a≠0，当x＝-3时，y＝0；当x＝4时，y＝0，则关于x的式子a (x-1)²＝-4b-c中x的值为.

查看试题解析
16. 已知m为整数，方程组 ${\begin{array}{l} 4 x - 3 y = 6 \\ 6 x + m y = 26 \end{array}$ 有正整数解，则m=.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt[3]{- 8} + \sqrt{16} - \sqrt{2 \frac{1}{4}}$ ；

(2)、 $\sqrt{3} (\sqrt{3} + \frac{1}{\sqrt{3}})$ .

查看试题解析
18. 计算：

(1)、 ${\begin{array}{l} 2 x - y = 5 \\ 3 x + 4 y = 2 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{2 u}{3} + \frac{3 v}{4} = \frac{1}{2} \\ \frac{4 u}{5} + \frac{5 v}{6} = \frac{7}{15} \end{array}$ .

查看试题解析
19. 如图，∠ABC＝∠ADC，BE，DF分别是∠ABC，∠ADC的角平分线，且∠2＝∠3，求证：BC//AD.

查看试题解析
20. 已知正实数x的平方根是a和a＋b.

(1)、当b＝6时，求a；

(2)、若a²x＋(a＋b)²x＝6，求x的值.

查看试题解析
21. 如图，△ABC中任意一点P(x₀ ， y₀)经平移后对应点为P′(x₀＋3，y₀＋4)，将△ABC作同样的平移得到△DEF，其中点A与点D，点B与点E，点C与点F分别对应，请解答下列问题：

(1)、直接写出点D、E、F的坐标；

(2)、画出 $△ D E F$ ，若 $A B = 2 \sqrt{2}$ ， $A C = B C = \sqrt{10}$ ， $A D = 5$ ， $D F =$ ， $C F =$ .

(3)、若将线段 $B C$ 沿某个方向进行平移得到线段MN，点 B(-1，-2)的对应点为 M ( m，0)，则点 C(0，1)的对应点 N 的坐标为.（用含 m的式子表示）

查看试题解析
22. 如图，长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨2000元的原料运回工厂，制成每吨5000元的产品运到B地，已知公路运价为2元/（吨·千米），铁路运价为1.5元/（吨·千米），且这两次运输共支出公路运输费14000元，铁路运输费87000元.

(1)、求：该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？

(2)、这批产品的销售款比原料费与运输费的和多多少元？

查看试题解析
23. 已知：两直线l₁ ， l₂满足l₁∥l₂ ，点C，点D在直线l₁上，点A，点B在直线l₂上，点P是平面内一动点，连接CP，BP，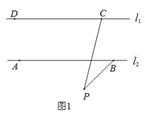

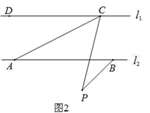(1)、如图 1，若点P在 l₁ ， l₂外部，则∠DCP、∠CPB、∠ABP之间满足什么数量关系？请你证明的这个结论；

(2)、如图 2，若点P在l₁ ， l₂外部，连接AC，则∠CAB、∠ACP、∠CPB、∠ABP之间满足什么数量关系？请你证明这个结论；（不能用三角形内角和为 180°）

(3)、若点P在 l₁ ， l₂内部，且在AC的右侧，则∠ACP﹑∠ABP﹑∠CAB﹑∠CPB之间满足什么数量关系？（不需证明）

查看试题解析
24. 如图 1，在平面直角坐标系中，已知点A(a，0)，B(b，0)，C(2，7)，连接 AC，交y轴于 D，且 $a = \sqrt[3]{- 125}$ ， ${(\sqrt{b})}^{2} = 5$ .

(1)、求点D的坐标.

(2)、如图 2，y轴上是否存在一点P，使得△ACP的面积与△ABC的面积相等？若存在，求点P的坐标，若不存在，说明理由.

(3)、如图 3，若 Q(m，n)是 x轴上方一点，且 $△ Q B C$ 的面积为20，试说明：7m＋3n是否为定值，若为定值，请求出其值，若不是，请说明理由.

查看试题解析