浙江省湖州市德清县2020届九年级下学期数学期中考试试卷
试卷更新日期:2020-05-26 类型:期中考试
一、选择题
-
1.
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
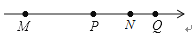 A、点M B、点N C、点P D、点Q2. 长兴是浙江省的北大门,与苏、皖两省接壤,位于太湖西南岸,全县区域面积1430平方公里,现有户籍人口约64万.将1430用科学记数法表示为( )A、0.143×104 B、1.43×103 C、14.3×102 D、143×103. 下列图形中,是中心对称图形又是轴对称图形的是( )A、
A、点M B、点N C、点P D、点Q2. 长兴是浙江省的北大门,与苏、皖两省接壤,位于太湖西南岸,全县区域面积1430平方公里,现有户籍人口约64万.将1430用科学记数法表示为( )A、0.143×104 B、1.43×103 C、14.3×102 D、143×103. 下列图形中,是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 在一次学生田径运动会上.参加男子跳高的15名运动员的成绩如下表所示:
4. 在一次学生田径运动会上.参加男子跳高的15名运动员的成绩如下表所示:成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
人数
1
2
4
3
3
2
这些运动员跳高成绩的中位数和众数是( )
A、1.65,1.70 B、1.70,1.70 C、1.70,1.65 D、3,45. 下列运算中,正确的是( )A、 B、 C、 D、6. 《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )A、 B、 C、 D、7. 如图,AB∥GH∥CD,点H在BC上,AC与BD交于点G,AB=2,CD=3,则GH长为( ) A、1 B、1.2 C、2 D、2.58. 解分式方程 ,正确的结果是( )A、x=0 B、x=1 C、x=2 D、无解9. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣ ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )
A、1 B、1.2 C、2 D、2.58. 解分式方程 ,正确的结果是( )A、x=0 B、x=1 C、x=2 D、无解9. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②3a+b<0;③﹣ ≤a≤﹣1;④a+b≥am2+bm(m为任意实数);⑤一元二次方程ax2+bx+c=n有两个不相等的实数根,其中正确的有( )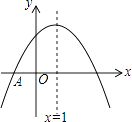 A、2个 B、3个 C、4个 D、5个10. 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
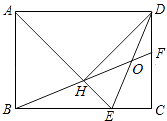
A、2个 B、3个 C、4个 D、5个10. 如图,在矩形ABCD中,AD= AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 因式分解: .12. 规定: ,如: ,若 ,则 =.13. 从分别标有1、2、3、4的四张卡片中,一次同时抽2张,其中和为奇数的概率是.14. 已知AB是⊙O的直径,弦CD⊥AB于点E,弦PQ∥AB交弦CD于点M,BE=18,CD=PQ=24,则OM的长为.
 15. 图甲是小明设计的带菱形图案的花边作品,该作品由形如图乙的矩形图案拼接而成(不重叠,无缝隙).图乙种, ,EF=4cm,上下两个阴影三角形的面积之和为54cm2 , 其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为cm
15. 图甲是小明设计的带菱形图案的花边作品,该作品由形如图乙的矩形图案拼接而成(不重叠,无缝隙).图乙种, ,EF=4cm,上下两个阴影三角形的面积之和为54cm2 , 其内部菱形由两组距离相等的平行线交叉得到,则该菱形的周长为cm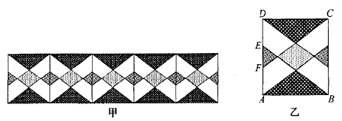 16. 如图,点A在双曲线y= 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为 ,则k的值为.
16. 如图,点A在双曲线y= 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为 ,则k的值为.
三、解答题
-
17. 如图,作业本上有这样一道填空题,其中有一部分被墨水污染了.若该题化简的结果为
.
 (1)、求被墨水污染的部分;(2)、原分式的值能等于 吗?为什么?18. 如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,CF⊥AB于点F.
(1)、求被墨水污染的部分;(2)、原分式的值能等于 吗?为什么?18. 如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,CF⊥AB于点F. (1)、求证:△BCF∽△CDE;(2)、若DE=3,求CF的长.19. 小明、小聪参加了100m跑的5期集训,每期集训结束市进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图:
(1)、求证:△BCF∽△CDE;(2)、若DE=3,求CF的长.19. 小明、小聪参加了100m跑的5期集训,每期集训结束市进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图:
根据图中信息,解答下列问题:
(1)、这5期的集训共有多少天?小聪5次测试的平均成绩是多少?(2)、根据统计数据,结合体育运动的实际,从集训时间和测试成绩这两方面,说说你的想法.20. 如图,直线 与反比例函数 的图象交于点 ,与x轴交于点B. (1)、求k的值及点B的坐标;(2)、过点B作 轴交反比例函数的图象于点D,求点D的坐标和 的面积;(3)、观察图象,写出当x>0时不等式 的解集.21. 已知在△ABC中,∠B=90o , 以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)、求k的值及点B的坐标;(2)、过点B作 轴交反比例函数的图象于点D,求点D的坐标和 的面积;(3)、观察图象,写出当x>0时不等式 的解集.21. 已知在△ABC中,∠B=90o , 以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E. (1)、求证:AC·AD=AB·AE;(2)、如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.22. 某竹制品加工厂根据市场调研结果,对该厂生产的一种新型竹制品玩具未来两年的销售进行预测,并建立如下模型:设第t个月,竹制品销售量为P(单位:箱),P与t之间存在如图所示函数关系,其图象是线段AB(不含点A)和线段BC的组合.设第t个月销售每箱的毛利润为Q(百元),且Q与t满足如下关系Q=2t+8(0≤t≤24).
(1)、求证:AC·AD=AB·AE;(2)、如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.22. 某竹制品加工厂根据市场调研结果,对该厂生产的一种新型竹制品玩具未来两年的销售进行预测,并建立如下模型:设第t个月,竹制品销售量为P(单位:箱),P与t之间存在如图所示函数关系,其图象是线段AB(不含点A)和线段BC的组合.设第t个月销售每箱的毛利润为Q(百元),且Q与t满足如下关系Q=2t+8(0≤t≤24).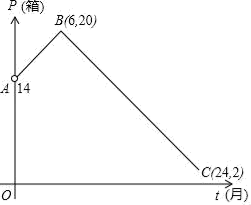 (1)、求P与t的函数关系式(6≤t≤24).(2)、该厂在第几个月能够获得最大毛利润?最大毛利润是多少?(3)、经调查发现,当月毛利润不低于40000且不高于43200元时,该月产品原材料供给和市场售最和谐,此时称这个月为“和谐月”,那么,在未来两年中第几个月为和谐月?23. 如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)、求P与t的函数关系式(6≤t≤24).(2)、该厂在第几个月能够获得最大毛利润?最大毛利润是多少?(3)、经调查发现,当月毛利润不低于40000且不高于43200元时,该月产品原材料供给和市场售最和谐,此时称这个月为“和谐月”,那么,在未来两年中第几个月为和谐月?23. 如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0). (1)、直接用含t的代数式分别表示:QB= , PD= .(2)、是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)、如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.24. 如图,在平面直角坐标系中,抛物线 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
(1)、直接用含t的代数式分别表示:QB= , PD= .(2)、是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;(3)、如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.24. 如图,在平面直角坐标系中,抛物线 与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H. (1)、求该抛物线的解析式;
(1)、求该抛物线的解析式;
(2)、当点P在直线BC上方时,请用含m的代数式表示PG的长度;(3)、在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.