湖北省孝感市云梦县2020届九年级下学期数学期中考试试卷
试卷更新日期:2020-05-26 类型:期中考试
一、选择题
-
1. – 的倒数是( )A、–5 B、5 C、– D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图,是一个长方体的三视图(单位: ),这个长方体的体积是( )
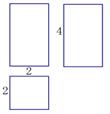 A、 B、 C、 D、4. 如图, , 平分 , 则 ( )
A、 B、 C、 D、4. 如图, , 平分 , 则 ( ) A、 B、 C、 D、5. 在平面直角坐标系中,将点 关于原点对称得到点 ,再将点 向左平移2个单位长度得到点 ,则点 的坐标是( )A、 B、 C、 D、6. 《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,若每人出8钱,则多了3钱;若每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为( )A、 B、 C、 D、7. 学校购回一批足球,为检测其质量,从中随机抽取8个足球,记录其质量如下表:
A、 B、 C、 D、5. 在平面直角坐标系中,将点 关于原点对称得到点 ,再将点 向左平移2个单位长度得到点 ,则点 的坐标是( )A、 B、 C、 D、6. 《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,若每人出8钱,则多了3钱;若每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为( )A、 B、 C、 D、7. 学校购回一批足球,为检测其质量,从中随机抽取8个足球,记录其质量如下表:质量
410
420
430
440
450
个数
2
1
1
3
1
则估计这批足球的平均质量和这组数据的方差分别是( )
A、430,20 B、430,200 C、440,30 D、440,3008. 如果 ,那么代数式 的值为( )A、 B、 C、1 D、49. 如图, 为等边三角形,点 从A出发,沿 作匀速运动,则线段 的长度y与运动时间x之间的函数关系大致是( ) A、
A、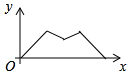 B、
B、 C、
C、 D、
D、 10. 如图, 中, , , ,D是线段AB上一个动点,以BD为边在 外作等边 .若F是DE的中点,则CF的最小值为( )
10. 如图, 中, , , ,D是线段AB上一个动点,以BD为边在 外作等边 .若F是DE的中点,则CF的最小值为( ) A、6 B、8 C、9 D、10
A、6 B、8 C、9 D、10二、填空题
-
11. 若代数式 有意义,则x的取值范围是.12. 不等式 的解集是.13. 为帮助国际社会抗击“新冠肺炎”,中国向127个国家或地区提供了防疫物资援助.据中国海关不完全统计,从3月1日至4月17日,中国对美国提供各类口罩18.64亿只.数据18.64亿用科学记数法表示为.14. 某校征集校运会会徽,遴选出甲、乙、丙三种图案,为了解何种图案更受欢迎,随机调查了该校100名学生,其中68名同学喜欢甲图案,若该校共有2000人,根据所学的统计知识可以估计该校喜欢甲图案的学生有人.15. 如图,航拍无人机从A处测得一幢建筑物顶部 的仰角为 ,测得底部C的俯角为 ,此时航拍无人机与该建筑物的水平距离AD为120m,那么该建筑物的高度BC约为m(结果保留整数, ).
 16. 如图,在 中, , , 与x轴交于点D, ,点A在反比例函数 的图象上,且y轴平分 ,求k=.
16. 如图,在 中, , , 与x轴交于点D, ,点A在反比例函数 的图象上,且y轴平分 ,求k=.
三、解答题
-
17. 计算:18. 如图, , ,AC,BD交于点O,求证: .
 19. 如图,已知矩形ABCD,用直尺和圆规进行如下操作:
19. 如图,已知矩形ABCD,用直尺和圆规进行如下操作:①以点A为圆心,以AD长为半径画弧,交BC于点E;
②连接AE,DE;
③以点E为圆心,以EC长为半径画弧,交AE于点F;
④连接DF.
根据以上操作,解答下列问题:
 (1)、线段DF与线段AE的位置关系是;(2)、若 ,求 的度数.20. 在甲、乙两个不透明的口袋中,分别有4个和3个大小、材质完全相同的小球,其中甲口袋中的小球上标有数字0,1,2,3,乙口袋中的小球上分别标有数字1,2,3,先从甲口袋中随机摸出一个小球,记下数字为m ,再从乙口袋中随机摸出一个小球,记下数字为n.(1)、请用列表法或画树状图的方法表示出所有 可能的结果;(2)、规定:若m.n都是方程 的解时,则小明获胜;若m.n都不是方程 的解时,则小宇获胜,问他们两人谁获胜的概率大?21. 已知关于X的一元二次方程 有两个不相等的实数根 , .(1)、若 为正整数,求 的值;(2)、若 , 满足 ,求A的值.22. 为迎接“五一”国际劳动节,某商场计划购进甲、乙两种品牌的 恤衫共100件,已知乙品牌每件的进价比甲品牌每件的进价贵30元,且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.(1)、求甲、乙两种品牌每件的进价分别是多少元?(2)、商场决定甲品牌以每件50元出售,乙品牌以每件100元出售.为满足市场需求,购进甲种品牌的数量不少于乙种品牌数量的4倍,请你确定获利最大的进货方案,并求出最大利润.23. 如图1,抛物线 过点 轴上的 和B点,交y轴于点C,点 该物上限一点,且 .
(1)、线段DF与线段AE的位置关系是;(2)、若 ,求 的度数.20. 在甲、乙两个不透明的口袋中,分别有4个和3个大小、材质完全相同的小球,其中甲口袋中的小球上标有数字0,1,2,3,乙口袋中的小球上分别标有数字1,2,3,先从甲口袋中随机摸出一个小球,记下数字为m ,再从乙口袋中随机摸出一个小球,记下数字为n.(1)、请用列表法或画树状图的方法表示出所有 可能的结果;(2)、规定:若m.n都是方程 的解时,则小明获胜;若m.n都不是方程 的解时,则小宇获胜,问他们两人谁获胜的概率大?21. 已知关于X的一元二次方程 有两个不相等的实数根 , .(1)、若 为正整数,求 的值;(2)、若 , 满足 ,求A的值.22. 为迎接“五一”国际劳动节,某商场计划购进甲、乙两种品牌的 恤衫共100件,已知乙品牌每件的进价比甲品牌每件的进价贵30元,且用120元购买甲品牌的件数恰好是购买乙品牌件数的2倍.(1)、求甲、乙两种品牌每件的进价分别是多少元?(2)、商场决定甲品牌以每件50元出售,乙品牌以每件100元出售.为满足市场需求,购进甲种品牌的数量不少于乙种品牌数量的4倍,请你确定获利最大的进货方案,并求出最大利润.23. 如图1,抛物线 过点 轴上的 和B点,交y轴于点C,点 该物上限一点,且 . (1)、抛物线的解析式为:;(2)、如图2,过点P作 轴交直线BC于点D,求点P在运动的过程中线段PD长度的最大值;(3)、如图3,若 ,在对称轴左侧的抛物线上是否存在点Q,使 ?若存在,请求出点Q的坐标,若不存在,请说明理由.
(1)、抛物线的解析式为:;(2)、如图2,过点P作 轴交直线BC于点D,求点P在运动的过程中线段PD长度的最大值;(3)、如图3,若 ,在对称轴左侧的抛物线上是否存在点Q,使 ?若存在,请求出点Q的坐标,若不存在,请说明理由.