湖北省鄂州市鄂城区2020届九年级下学期数学期中考试试卷
试卷更新日期:2020-05-26 类型:期中考试
一、选择题
-
1. 在实数|﹣3|,﹣2,0,π中,最小的数是( )
A、|﹣3| B、﹣2 C、0 D、π2. 改革开放四十年来,北京市民的收入随着经济水平的发展而显著提高. 从储蓄数据来看,2017年北京市民的人民币储蓄存款余额约为2 980 000 000 000元,大致为1978年的3200倍. 将2 980 000 000 000用科学记数法表示应为( )A、 B、 C、 D、3. 如图, , , ,则 的度数为( )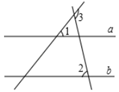 A、 B、 C、 D、4. 如图所示的几何体,它的左视图是( )
A、 B、 C、 D、4. 如图所示的几何体,它的左视图是( ) A、
A、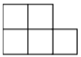 B、
B、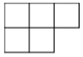 C、
C、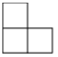 D、
D、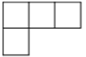 5. 下列运算正确的是( )A、 B、 C、 D、6. 为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:则关于“户外时间活动时间”这组数据的众数、中位数、平均数分别是( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:则关于“户外时间活动时间”这组数据的众数、中位数、平均数分别是( )户外活动的时间(小时)
1
2
3
6
学生人数(人)
2
2
4
2
A、3、3、3 B、6、2、3 C、3、3、2 D、3、2、37. 如图,点 是反比例函数 的图象上任意一点, 轴交反比例函数 的图象于点B,以AB为边作 ,其中C,D在x轴上,则 为( )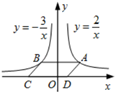 A、2.5 B、3.5 C、4 D、58. 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′( a+1, b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )A、S1 S2 B、S1 S2 C、S1=2S2 D、S1=4S29. 如图,等边 边长为a,点O是 的内心, ,绕点O旋转 ,分别交线段AB,BC于D,E两点,连接DE,给出下列四个结论:① 形状不变;② 的面积最小不会小于四边形 的面积的四分之一;③四边形 的面积始终不变;④ 周长的最小值为1.5a.上述结论中正确的个数是( )
A、2.5 B、3.5 C、4 D、58. 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′( a+1, b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )A、S1 S2 B、S1 S2 C、S1=2S2 D、S1=4S29. 如图,等边 边长为a,点O是 的内心, ,绕点O旋转 ,分别交线段AB,BC于D,E两点,连接DE,给出下列四个结论:① 形状不变;② 的面积最小不会小于四边形 的面积的四分之一;③四边形 的面积始终不变;④ 周长的最小值为1.5a.上述结论中正确的个数是( )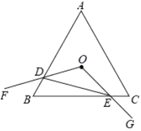 A、4 B、3 C、2 D、110. 如图,抛物线 的对称轴为直线x=-2,与x轴的一个交点在 和 之间,其部分图象如图所示.则下列结论:① ;② ;③ ;④ ( 为实数);⑤点 , , 是该抛物线上的点,则 ,其中,正确结论的个数是( )
A、4 B、3 C、2 D、110. 如图,抛物线 的对称轴为直线x=-2,与x轴的一个交点在 和 之间,其部分图象如图所示.则下列结论:① ;② ;③ ;④ ( 为实数);⑤点 , , 是该抛物线上的点,则 ,其中,正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 函数y= 的自变量x的取值范围是.12. 如图,在圆中, , ,则 的度数是.
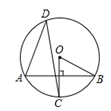 13.
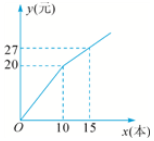
13.小明到超市买练习本,超市正在打折促销:购买10本以上,从第11本开始按标价打折优惠,买练习本所花费的钱数y(元)与练习本的个数x(本)之间的关系如图所示,那么在这个超市买10本以上的练习本优惠折扣是 折.
 14. 在平面直角坐标系中,M、N、C三点的坐标分别为 , , ,点A为线段MN上的一个动点,连接AC,过点A作 交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为 ,则b的取值范围是.15. 已知:y关于x的函数 的图象与坐标轴只有两个不同的交点A、B,P点坐标为 ,则 的面积为.16. 如图,已知 ,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE.点P,C,E在一条直线上, ,M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为.
14. 在平面直角坐标系中,M、N、C三点的坐标分别为 , , ,点A为线段MN上的一个动点,连接AC,过点A作 交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为 ,则b的取值范围是.15. 已知:y关于x的函数 的图象与坐标轴只有两个不同的交点A、B,P点坐标为 ,则 的面积为.16. 如图,已知 ,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE.点P,C,E在一条直线上, ,M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为.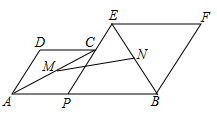
三、解答题
-
17. 先化简,再计算: ,其中x= .18. 如图,在矩形ABCD中, ,点 ,F分别在BC,CD上,将 沿AE折叠,使点B落在AC上的点 处,又将 沿EF折叠,使点C落在直线 与AD的交点 处.
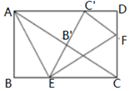 (1)、求证:点C在 的角平分线上;(2)、求 的长.19. 去年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
(1)、求证:点C在 的角平分线上;(2)、求 的长.19. 去年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:等级
成绩( )
频数(人数)
6
24
9
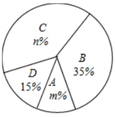
根据以上信息,解答以下问题:
(1)、表中的x=;(2)、扇形统计图中m= , n= , 等级对应的扇形的圆心角为度;(3)、该校准备从上述获得A等级6名学生中选取两人做为学校“五好小公民”志愿者,已知这6人中有3名男生(用 , , 表示)和3名女生(用 , , 表示),请用列表或画树状图的方法求恰好选取的是 和 的概率.20. 已知关于X的一元二次方程 .(1)、求证:此方程总有两个实数根;(2)、若此方程有一个根大于-3且小于-1,k为整数,求k的值.21. 如图(1)是一种简易台灯,在其结构图(2)中灯座为△ABC(BC伸出部分不计),A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.(参考数据:sin15°=0.26,cos15°=0.97,tan15°=0.27,sin30°=0.5,cos30°=0.87,tan30°=0.58.)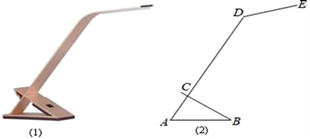 (1)、求DE与水平桌面(AB所在直线)所成的角;(2)、求台灯的高(点E到桌面的距离,结果精确到0.1cm).22. 如图,在 中, ,AD为 的平分线,点O在AB上, 经过点A,D两点,与AC,AB分别交于点E,F.
(1)、求DE与水平桌面(AB所在直线)所成的角;(2)、求台灯的高(点E到桌面的距离,结果精确到0.1cm).22. 如图,在 中, ,AD为 的平分线,点O在AB上, 经过点A,D两点,与AC,AB分别交于点E,F. (1)、求证:BC与 相切;(2)、若 , ,求 的半径r和BC的长.23. 某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15.
(1)、求证:BC与 相切;(2)、若 , ,求 的半径r和BC的长.23. 某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15. (1)、第 25 天,该商家的成本是元,获得的利润是元;(2)、设第 x 天该商家出售该产品的利润为 w 元.
(1)、第 25 天,该商家的成本是元,获得的利润是元;(2)、设第 x 天该商家出售该产品的利润为 w 元.①求 w 与 x 之间的函数关系式;
②求出第几天的利润最大,最大利润是多少?
24. 如图,以D为顶点的抛物线 交x轴于点A, ,交y轴于点 . (1)、求抛物线的解析式;(2)、在直线BC上有一点P,使 的值最小,求点P的坐标;(3)、在 轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与 相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在直线BC上有一点P,使 的值最小,求点P的坐标;(3)、在 轴上是否存在一点Q,使得以A,C,Q为顶点的三角形与 相似?若存在,请求出点Q的坐标;若不存在,请说明理由.