湖北省武汉市东湖高新区2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2020-05-26 类型：期中考试

进入出卷网下载

一、选择题

1. 若式子 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（）

A、x≠1 B、x＞1 C、x≥1 D、x≤1

查看试题解析
2. 下列二次根式是最简二次根式的是（）.

A、 $\sqrt{8}$ B、 $\sqrt{7}$ C、 $\sqrt{0.3}$ D、 $\sqrt{\frac{1}{5}}$

查看试题解析
3. 下列各组数中不能作为直角三角形的三边长的是（）

A、6，8，10 B、7，24，25 C、1.5，2，3 D、9，12，15

查看试题解析
4. 下列命题中，是假命题的是（）

A、平行四边形的两组对边分别相等 B、两组对边分别相等的四边形是平行四边形 C、矩形的对角线相等 D、对角线相等的四边形是矩形

查看试题解析
5. 如图，一竖直的木杆在离地面4米处折断，木杆顶端落在地面离木杆底端3米处，木杆折断之前的高度为（）.

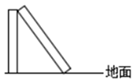A、7米 B、8米 C、9米 D、12米

查看试题解析
6. 如图，Rt△ABC中，∠ACB＝90°，以AC，BC为直径作半圆S₁和S₂ ，且S₁+S₂＝2π，则AB的长为（）

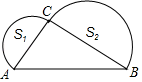A、16 B、8 C、4 D、2

查看试题解析
7. 如图，菱形ABCD中，对角线AC＝6，BD＝8，M、N分别是BC、CD上的动点，P是线段BD上的一个动点，则PM＋PN的最小值是（）

A、 $\frac{9}{5}$ B、 $\frac{12}{5}$ C、 $\frac{16}{5}$ D、 $\frac{24}{5}$

查看试题解析
8. 观察下列式子： $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 \frac{1}{2}$ ； $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 \frac{1}{6}$ ； $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 \frac{1}{12}$ ；……，根据此规律，若 $\sqrt{1 + \frac{1}{a^{2}} + \frac{1}{b^{2}}} = 1 \frac{1}{90}$ ，则a²＋b²的值为（）.

A、110 B、164 C、179 D、181

查看试题解析
9. 如图，正方形ABDC中，AB＝6，E在CD上，DE＝2，将△ADE沿AE折叠至△AFE，延长EF交BC于G，连AG、CF，下列结论：①△ABG≌△AFG；②BG＝CG；③AG∥CF；④ $S_{Δ}$ _FCG＝3，其中正确的有（）.

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

10. 化简： $\sqrt{12}$ =； ${(- \sqrt{5})}^{2}$ ＝； $\sqrt{\frac{4}{9}}$ ＝.

查看试题解析
11. 如图，点P（－2，3），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的坐标为.

查看试题解析
12. 已知 $\sqrt{18 - n}$ 是整数，自然数n的最小值为.

查看试题解析
13. 如图，O是矩形ABCD对角线的交点，AE平分∠BAD，∠OAE＝15°，则∠AEO的度数为.

查看试题解析
14. 如图，等腰三角形纸片ABC中，AD⊥BC与点D，BC=2，AD= $\sqrt{3}$ ，沿AD剪成两个三角形.用这两个三角形拼成平行四边形，该平行四边形中较长对角线的长为.

查看试题解析
15. 如图，矩形ABCD中，AB＝12，点E是AD上的一点，AE＝6，BE的垂直平分线交BC的延长线于点F，连接EF交CD于点G.若G是CD的中点，则BC的长是.

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{18} - \sqrt{32} + \sqrt{8}$

(2)、 $\sqrt{\frac{2}{3}} \times \sqrt{\frac{27}{2}}$

查看试题解析
17. 已知a＝ $2 + \sqrt{3}$ ，b＝ $2 - \sqrt{3}$ 求下列各式的值：

(1)、a²＋2ab＋b²

(2)、a²－b²

查看试题解析
18. 如图，在平行四边形ABCD中，AE＝CF，求证：四边形BFDE是平行四边形．

查看试题解析
19. 如图，正方形网格中每个小正方形边长均为1，每个小正方形的顶点叫格点，以格点为顶点按下列要求画图：

(1)、画一个△ABC，使AC= $\sqrt{5}$ ，BC= $2 \sqrt{5}$ ，AB=5；

(2)、若点D为AB的中点，则CD的长是；

(3)、在（2）的条件下，直接写出点D到AC的距离为.

查看试题解析
20. 如图，在平行四边形ABCD中，AC、BD交于点O，又M、N分别是OA、OC的中点.

(1)、求证：BM＝DN；

(2)、若AO＝BD，试判断四边形MBND的形状，并证明你的结论.

查看试题解析
21. △ABC中，BC＝8，以AC为边向外作等边△ACD.

(1)、如图①，△ABE是等边三角形，若AC＝6，∠ACB＝30°，求CE的长；

(2)、如图②，若∠ABC＝60°，AB＝4，求BD的长.

查看试题解析
22. 如图，在四边形ABCD中，AB∥CD，∠ABC=∠BCD=90°，AD=10cm，BC=8cm，CD=16cm.点P从点A出发，以每秒3cm的速度沿折线段AB—BC—CD运动，点Q从点D出发，以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发，设运动时间为t秒（ $0 \leq t \leq 8$ ）.

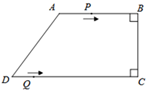(1)、求AB的长；

(2)、当四边形PBQD为平行四边形时，求四边形PBQD的周长；

(3)、在点P运动过程中，当 $t =$ 秒的时候，使得△BPD的面积为20cm².

查看试题解析
23. 平面直角坐标系中有正方形AOBC，O为坐标原点，点A、B分别在y轴、x轴正半轴上，点P、E、F分别为边BC、AC、OB上的点，EF⊥OP于M.

(1)、如图1，若点E与点A重合，点A坐标为（0，8），OF＝3，求P点坐标；

(2)、如图2，若点E与点A重合，且P为边BC的中点，求证：CM=2CP；

(3)、如图3，若点M为线段OP的中点，连接AB交EF于点N，连接NP，试探究线段OP与NP的数量关系，并证明你的结论.

查看试题解析