备考2020年初中数学二轮复习拔高训练卷 专题12 统计与概率
试卷更新日期：2020-05-25 类型：二轮复习
一、单选题
-
1. 下列调查中，适合采用全面调查（普查）方式的是（ ）A、对渭河水质情况的调查 B、了解新冠肺炎确诊病人同机乘客的健康情况 C、对超市粽子质量情况的调查 D、对某类烟花爆竹燃放安全情况的调查2. 下列说法正确的是（ ）A、“367人中有2人同月同日生”为必然事件 B、检测某批次灯泡的使用寿命，适宜用全面调查 C、可能性是1%的事件在一次试验中一定不会发生 D、数据3，5，4，1，-2的中位数是43. 某中学对学生进行各学科期末综合评价，评价分平时成绩和期末实考成绩两部分，平时成绩与期末实考成绩按4：6计算作为期末评价结果，若小明数学的平时成绩为85分，期末实考成绩为90分，则他的数学期末评价结果为（ ）A、89 分 B、88 分 C、87 分 D、86 分4. 为了参加市中学生篮球运动会，一支校篮球队准备购买10双运动鞋，各种尺码统计如下表：
尺码（厘米）
25
25.5
26
26.5
27
购买量（双）
1
2
3
2
2
则这10双运动鞋尺码的众数和中位数分别为（ ）
A、25.5厘米，26厘米 B、26厘米，25.5厘米 C、25.5厘米，25.5厘米 D、26厘米，26厘米5. 某班30名学生的身高情况如下表
关于身高的统计量中，不随x、y的变化而变化的有（ ）
A、众数，中位数 B、中位数，方差 C、平均数，方差 D、平均数，众数6. 某住宅小区六月份1日至5日每天用水量变化情况如图所示．那么这5天用水量的中位数是（ ）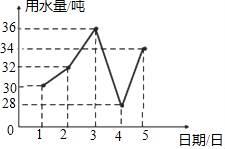
A、30吨 B、36吨 C、32吨 D、34吨7. 点点同学对数据26，36，46，
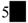，52进行统计分析，发现其中一个两位数的个位数字被墨水涂污看不到了，则计算结果与被涂污数字无关的是（ ） A、平均数 B、中位数 C、方差 D、标准差8. 若一组数据x1+1，x2+1，…，xn+1的平均数为16，方差为2，则另一组数据x1+2，x2+2，…，xn+2的平均数和方差分别为（ ）A、17，2 B、 17，3 C、16，2 D、16，39. 图书管理员在整理阅览室的课外书籍时，将其中甲、乙、丙三类书籍的有关数据制成如图所示不完整的统计图，已知甲类书有30本，则丙类书的本数是（ ）
A、90 B、144 C、200 D、8010. 下列事件中，属于不可能事件的是（ ）A、某个数的绝对值大于0 B、任意一个五边形的外角和等于540° C、某个数的相反数等于它本身 D、长分别为3，4，6的三条线段能围成一个三角形11. 有编号为Ⅰ，Ⅱ，Ⅲ的3个信封，现将编号为Ⅰ，Ⅱ的两封信，随机地放入其中两个信封里，则信封与信编号都相同的概率为（ ）A、 B、 C、 D、12. 小明要给朋友小林打电话，电话号码是七位正整数，他只记住了电话号码的前四位，后三位是由3，6，7三个数字组成的，但具体顺序不能确定，那么小明第一次就拨对的概率是（ ）A、 B、 C、 D、二、填空题
-
13. 已知一组数据是整数，其中最大值是242，最小数据是198，若把这组数据组距定为5，则可以分成组。14. 一组数据1，x，4，6，2的中位数是x，唯一的众数也是x，则整数x的值可能是 。15. 一组数据：1，2，3，4，5的方差为 ．16. 据统计，某车间10名员工的日平均生产零件个数为8个，方差为2.5个²。引入新技术后，每名员工每天都比原先多生产1个零件，则现在日平均生产零件个数为个，方差为个2。17. 有五张背面完全相同的纸质卡片，其正面分别标有数：6、 、 、-2、 。将它们背面朝上洗匀后，从中随机抽取一张卡片，则其正面的数比3小的概率是。18. 一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使不知道密码的人一次就拨对密码的概率小于 ，则密码的位数至少需要位。19. 如图，把大正方形平均分成9个小正方形，其中有2个小正方形已被涂黑，在剩余的7个白色小正方形中任选一个也涂黑，则使整个涂黑部分成为轴对称图形的概率是 ．
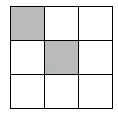
三、解答题
-
20. 有三张正面分别写有数字1，3，4的卡片，它们的背面完全相同，将这三张卡片背面朝上洗匀后随机抽取一张，以其正面的数字作为a的值，把方程组 的解记为平面直角坐标系中点A的坐标(x，y)，求点A在第四象限的概率。21. 孙老师在上《等可能事件的概率》这节课时，给同学们提出了一个问题：“如果同时随机投掷两枚质地均匀的骰子，它们朝上一面的点数和是多少的可能性最大？”同学们展开讨论，各抒己见，其中小芳和小超两位同学给出了两种不同的回答。小芳认为6的可能性最大，小超认为7的可能性最大。你认为他们俩的回答正确吗？请用列表或画树状图等方法加以说明。
（骰子：六个面上分别刻有1，2，3，4，5，6个小圆点的小正方体。）
22. 有两个构造完全相同（除所标数字外）的转盘A、B，游戏规定，转动两个转盘各一次，指向大的数字获胜.现由你和小明各选择一个转盘游戏，你会选择哪一个，为什么？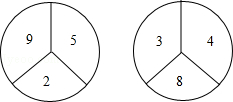
23. 某商场开业，为了活跃气氛，用红、黄、蓝三色均分的转盘设计了两种抽奖方案，凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖.方案一：转动转盘一次，指针落在红色区域可领取一份奖品；
方案二：转动转盘两次，指针落在不同颜色区域可领取一份奖品，你会选择哪个方案？请用相关的数学知识说明理由.
24. 我市为加强学生的安全意识，组织了全市学生参加安全知识竞赛，为了解此次知识竞赛成绩的情况，随机抽取了部分参赛学生的成绩，整理并制作出如下的不完整的统计表和统计图，如图所示，请根据图表信息解答以下问题．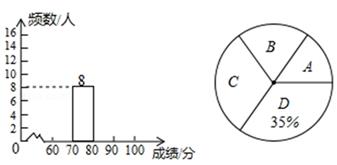
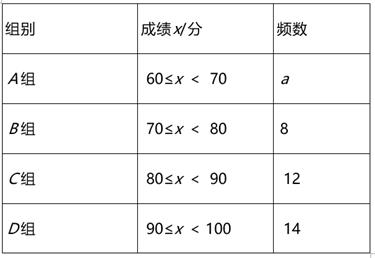(1)、一共抽取了个参赛学生的成绩；表中a＝；(2)、补全频数分布直方图；(3)、计算扇形统计图中“B”对应的圆心角度数；(4)、若成绩在80分以上（包括80分）的为“优”等，则所抽取学生成绩为“优”的占所抽取学生的百分比是多少？25. 某中学初三（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如下的两幅不完整的统计图(如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：
(1)、初三（1）班的学生人数为 ， 并把条形统计图补充完整；(2)、扇形统计图中m= ， n= ， 表示“足球”的扇形的圆心角是度；(3)、排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．