备考2020年初中数学二轮复习拔高训练卷 专题11 视图与投影
试卷更新日期:2020-05-25 类型:二轮复习
一、单选题
-
1. 下列几何体的主视图与左视图不相同的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图所示的几何体的左视图是( )
2. 如图所示的几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 左下图是由四个相同的小立方块搭成的几何体,这个几何体的左视图是( )
3. 左下图是由四个相同的小立方块搭成的几何体,这个几何体的左视图是( )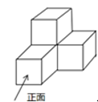 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列四个几何体中,左视图为圆的是( )A、
4. 下列四个几何体中,左视图为圆的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列对如图物体三视图描述正确的是( )
5. 下列对如图物体三视图描述正确的是( )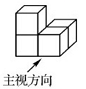 A、左视图和俯视图相同 B、主视图和左视图相同 C、主视图和俯视图相同 D、三视图都相同6. 如图所示的几何体,其主视图中正方形的个数是( )
A、左视图和俯视图相同 B、主视图和左视图相同 C、主视图和俯视图相同 D、三视图都相同6. 如图所示的几何体,其主视图中正方形的个数是( ) A、4 B、3 C、2 D、17. 如右图所示,该几何体由两个圆柱分别从纵横两个方向嵌入一个正方体形成的,它的主视图是( )
A、4 B、3 C、2 D、17. 如右图所示,该几何体由两个圆柱分别从纵横两个方向嵌入一个正方体形成的,它的主视图是( )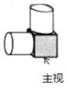 A、
A、 B、
B、 C、
C、 D、
D、 8. 如图所示的几何体的俯视图是( )
8. 如图所示的几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图是一空心圆柱,其主视图正确的是( )
9. 如图是一空心圆柱,其主视图正确的是( )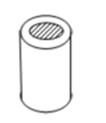 A、
A、 B、
B、 C、
C、 D、
D、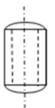 10. 如图所示图形,下列选项中不是图中几何体的三视图的是( )
10. 如图所示图形,下列选项中不是图中几何体的三视图的是( ) A、
A、 B、
B、 C、
C、 D、
D、 11. 如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )
11. 如图是由5个完全相同的小正方体搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )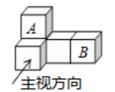 A、左视图会发生改变,其他视图不变 B、俯视图会发生改变,其他视图不变 C、主视图会发生改变,其他视图不变 D、三种视图都会发生改变12. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、3
A、左视图会发生改变,其他视图不变 B、俯视图会发生改变,其他视图不变 C、主视图会发生改变,其他视图不变 D、三种视图都会发生改变12. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、3二、填空题
-
13. 一个几何体由若干大小相同的小立方块搭成,如图所示的分别是从它的正面、左面看到的图形,则搭成该几何体最多需要个小立方块.
 14. 一个几何体的主视图和俯视图如图所示,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,m+n= .
14. 一个几何体的主视图和俯视图如图所示,若这个几何体最多有m个小正方体组成,最少有n个小正方体组成,m+n= .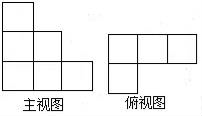 15. 一个小立方体的六个面分别标有数字1、2. 3、4、5、6,从三个不同的方向看到的情形如图所示,则数字6的对面是.
15. 一个小立方体的六个面分别标有数字1、2. 3、4、5、6,从三个不同的方向看到的情形如图所示,则数字6的对面是. 16. 甲、乙两人在太阳光下行走,同一时刻他们的身高与其影长之比的关系是17. 工人师傅要制造某一工件,他想知道工件的高,需要看到三视图中的或 .18. 小明的身高为1.6米,他在阳光下的影长为0.8米,同一时刻,测得校园的旗杆的影长为4.5米,则该旗杆的高为米.19. 如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为.
16. 甲、乙两人在太阳光下行走,同一时刻他们的身高与其影长之比的关系是17. 工人师傅要制造某一工件,他想知道工件的高,需要看到三视图中的或 .18. 小明的身高为1.6米,他在阳光下的影长为0.8米,同一时刻,测得校园的旗杆的影长为4.5米,则该旗杆的高为米.19. 如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为. 20. 已知某几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的左视图的面积为.
20. 已知某几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的左视图的面积为.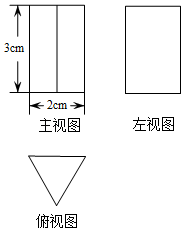
三、解答题
-
21. 如图是某工件的三视图,求此工件的全面积和体积.
 22. 如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
22. 如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.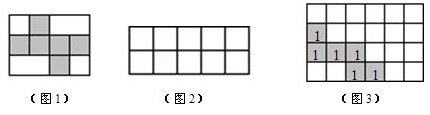 (1)、计算图1长方形的面积;(2)、小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);(3)、如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.23. 如图,在一间黑屋里用一白炽灯照射一个球,
(1)、计算图1长方形的面积;(2)、小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);(3)、如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.23. 如图,在一间黑屋里用一白炽灯照射一个球,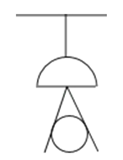 (1)、球在地面上的阴影是什么形状?(2)、当把白炽灯向上移时,阴影的大小会怎样变化?(3)、若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?24. 如图所示,点P表示广场上的一盏照明灯.
(1)、球在地面上的阴影是什么形状?(2)、当把白炽灯向上移时,阴影的大小会怎样变化?(3)、若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?24. 如图所示,点P表示广场上的一盏照明灯.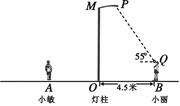 (1)、请你在图中画出小敏在照明灯照射下的影子(用线段表示);(2)、若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).
(1)、请你在图中画出小敏在照明灯照射下的影子(用线段表示);(2)、若小丽到灯柱MO的距离为4.5米,照明灯P到灯柱的距离为1.5米,小丽目测照明灯P的仰角为55°,她的目高QB为1.6米,试求照明灯P到地面的距离(结果精确到0.1米).(参考数据:tan55°≈1.428,sin55°≈0.819,cos55°≈0.574)
25. 如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB. (1)、求两个路灯之间的距离;(2)、当小华走到路灯B的底部时,他在路灯A下的影长是多少?
(1)、求两个路灯之间的距离;(2)、当小华走到路灯B的底部时,他在路灯A下的影长是多少?