安徽省宿州市萧县2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-05-25 类型:期末考试
一、选择题
-
1. 下列计算中,正确的是( )A、-a(3a2-1)=-3a3-a B、(a-b)2=a2-b2 C、(-2a-3)(2a-3)=9-4a2 D、(2a-b)2=4a2-2ab+b22. 计算(-a-b)2等于( )A、a2+b2 B、a2-b2 C、a2+2ab+b2 D、a2-2ab+b23. 下列四个图中,∠1和∠2是对顶角的图的个数是( )
 A、0个 B、1个 C、2个 D、3个4. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2的度数等于( )
A、0个 B、1个 C、2个 D、3个4. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2的度数等于( ) A、50° B、30° C、20 D、15°5. 已知等腰三角形的一边为5cm,另一边为6cm,那么这个三角形的周长为( )A、16cm B、17cm C、16cm或17cm D、以上都不对6. 如图,E是∠BAC的平分线AD上任意一点,且AB=AC,则图中全等三角形有( )
A、50° B、30° C、20 D、15°5. 已知等腰三角形的一边为5cm,另一边为6cm,那么这个三角形的周长为( )A、16cm B、17cm C、16cm或17cm D、以上都不对6. 如图,E是∠BAC的平分线AD上任意一点,且AB=AC,则图中全等三角形有( )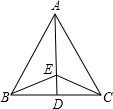 A、4对 B、3对 C、2对 D、1对7. 如图所示转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等,四位同学各自发表了下述见解:
A、4对 B、3对 C、2对 D、1对7. 如图所示转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等,四位同学各自发表了下述见解:甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的机会与停在偶数号扇形的机会相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大.
其中,你认为正确的见解有( )
 A、1个 B、2个 C、3个 D、4个8. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.下列说法不正确的是( )
A、1个 B、2个 C、3个 D、4个8. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.下列说法不正确的是( )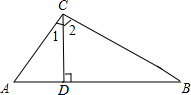 A、与∠1互余的角只有∠2 B、∠A与∠B互余 C、∠1=∠B D、若∠A=2∠1,则∠B=30°9. 有一游泳池注满水,现按一定的速度将水排尽,然后进行清扫,再按相同的速度注满清水,使用一段时间后,又按相同的速度将水排尽,则游泳池的存水量V(立方米)随时间t(小时)变化的大致图象可以是( )A、
A、与∠1互余的角只有∠2 B、∠A与∠B互余 C、∠1=∠B D、若∠A=2∠1,则∠B=30°9. 有一游泳池注满水,现按一定的速度将水排尽,然后进行清扫,再按相同的速度注满清水,使用一段时间后,又按相同的速度将水排尽,则游泳池的存水量V(立方米)随时间t(小时)变化的大致图象可以是( )A、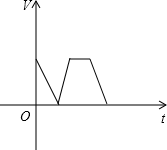 B、
B、 C、
C、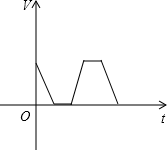 D、
D、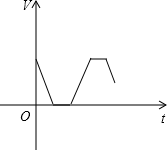 10. 将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( )
10. 将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( ) A、
A、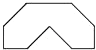 B、
B、 C、
C、 D、
D、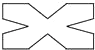
二、填空题
-
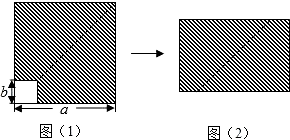
11. 生物学家发现一种病毒的长度约为0.000043mm,这个数用科学记数法可以表示为mm.12. 单项选择题是数学试题的重要组成部分,当你遇到不懂做的情况时,如果你随便选一个答案(假设每个题目有4个备选答案),那么你答对的可能性为 .13. 在边长为a的正方形纸片中剪去一个边长为b的小正方形(a>b)(如图(1)),把余下的部分沿虚线剪开,拼成一个矩形(如图(2)),分别计算这两个图形阴影部分的面积,可以验证的乘法公式是 . (用字母表示)
 14. 如图,AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB,AB=DE,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的方法,可以简写为 .
14. 如图,AB⊥CF,垂足为B,AB∥DE,点E在CF上,CE=FB,AB=DE,依据以上条件可以判定△ABC≌△DEF,这种判定三角形全等的方法,可以简写为 . 15. 如图,△ABC中,AB=AC,∠A=40°,DE垂直平分AC交AB于E,则∠BCE=
15. 如图,△ABC中,AB=AC,∠A=40°,DE垂直平分AC交AB于E,则∠BCE=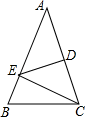 16. 在原有运算法则中,我们补充新运算法则“*”如下:当a≥b时,a*b=(-b)2;当a<b时,a*b=-(a2)3 . 则当x=2时,(x*1)x-(x*3)= .
16. 在原有运算法则中,我们补充新运算法则“*”如下:当a≥b时,a*b=(-b)2;当a<b时,a*b=-(a2)3 . 则当x=2时,(x*1)x-(x*3)= .三、解答题
-
17. 计算:(x-y)2-(x+y)(x-y)18. 如图,在正方形网格上有一个△ABC,作△ABC关于直线MN的对称图形(不写作法).
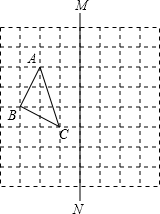 19. 填空完成下列推理过程
19. 填空完成下列推理过程已知:如图,BD⊥AC,EF⊥AC,点D、F分别是垂足,∠1=∠4.
试说明:∠ADG=∠C
解:∵BD⊥AC,EF⊥AC(已知)
∴∠2=90°∠3=90°(垂直的定义)
∴∠2=∠3(等量代换)
∴BD∥EF
∴∠4=∠5(两直线平行同位角相等)
∵∠1=∠4(已知)
∠1=∠5
∴DG∥CB(内错角相等两直线平行)
∴∠ADG=∠C
 20. 小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).
20. 小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).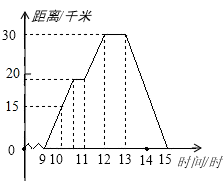 (1)、图象表示了哪两个变量的关系?(2)、10时,他离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、他可能在哪段时间内休息,并吃午餐?(5)、他由离家最远的地方返回时的平均速度是多少?21. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E、D,AD=2.6cm,DE=1.2cm,求BE的长.
(1)、图象表示了哪两个变量的关系?(2)、10时,他离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、他可能在哪段时间内休息,并吃午餐?(5)、他由离家最远的地方返回时的平均速度是多少?21. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E、D,AD=2.6cm,DE=1.2cm,求BE的长. 22. 小明所在年级有12个班,每班40名同学.学校将从该年级随机抽出一个班组建运动会入场式鲜花队,并在该班中再随机抽出1名同学当鲜花队的引导员.问:(1)、小明当鲜花队的队员的概率是多少?(2)、小明抽中引导员的概率是多少?(3)、若小明所在班被抽中了鲜花队,那么小明抽中引导员的概率是多少?23. 尺规作图:已知三角形的两角及其夹边,求作这个三角形.
22. 小明所在年级有12个班,每班40名同学.学校将从该年级随机抽出一个班组建运动会入场式鲜花队,并在该班中再随机抽出1名同学当鲜花队的引导员.问:(1)、小明当鲜花队的队员的概率是多少?(2)、小明抽中引导员的概率是多少?(3)、若小明所在班被抽中了鲜花队,那么小明抽中引导员的概率是多少?23. 尺规作图:已知三角形的两角及其夹边,求作这个三角形.
已知:∠α,∠β,线段a.
求作:△ABC,使得∠A=∠α,∠B=∠β,AB=a.
(不要求写作法,保留作图痕迹即可.)
24. 如图:小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了20步到达一棵树C处,接着再向前走了20步到达D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了100步. (1)、根据题意,画出示意图;(2)、如果小刚一步大约50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.
(1)、根据题意,画出示意图;(2)、如果小刚一步大约50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.四、计算题(本大题共 1 小题,共 6 分)
-
25. 先化简,再求值:(3x+2)(3x-2)-5x(x-1)-(2x-1)2 , 其中x=- .