安徽省铜陵市2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-25 类型：期末考试

进入出卷网下载

一、选择题

1. 如果a＞b，那么下列结论一定正确的是（　　）

A、a-3＜b-3 B、3-a＞3-b C、 $- \frac{a}{3} < - \frac{b}{3}$ D、-3a＞-3b

查看试题解析
2. 下列实数中，是有理数的是（　　）

A、 $\sqrt{- 8}$ B、2.020020002 C、 $\sqrt[3]{4}$ D、 $\frac{1}{4}$ π

查看试题解析
3. 下列调查中，最适合采用全面调查（普查）的是（　　）

A、对“神舟十一号”载人飞船各零部件质量检查 B、长江铜陵段水质检测 C、了解某批次节能灯的使用寿命 D、了解热播电视剧《人民的名义》的收视率

查看试题解析
4. 在平面直角坐标系内，点P（2m+1，m-3）不可能在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如果3a-21和2a+1是正实数m的两个不同的平方根，那么 $\sqrt{m}$ 的值为（　　）

A、2 B、3 C、4 D、9

查看试题解析
6. 不等式组 ${\begin{array}{l} x - 1 ⩾ 0 \\ 4 - 2 x > 0 \end{array}$ 的解集在数轴上表示为（　　）

A、 B、 C、 D、

查看试题解析
7. 关于x、y的二元一次方程组 ${\begin{array}{l} x + y = m + 1 \\ 2 x + y = 3 \end{array}$ 中，未知数x、y满足x+y＞-3，则m的取值范围是（　　）

A、m≥-4 B、m＞-4 C、m＜-4 D、m≤-4

查看试题解析
8. 如图，点E在BC延长线上，下列条件中，不能推断AB∥CD的是（　　）

A、∠4=∠3 B、∠1=∠2 C、∠B=∠5 D、∠B+∠BCD=180°

查看试题解析
9. 根据图中提供的信息，可知一个杯子的价格是（　　）

A、51元 B、35元 C、8元 D、7.5元

查看试题解析
10. 如图，AB⊥BC，AE平分∠BAD交BC于点E，AE⊥DE，∠1+∠2=90°，M、N分别是BA、CD延长线上的点，∠EAM和∠EDN的平分线交于点F，∠F的度数为（　　）

A、120° B、135° C、150° D、不能确定

查看试题解析

二、填空题

11. 若点P(a，b)在第四象限，则点M(b－a，a－b)在第象限.

查看试题解析
12. 一个样本容量为80的抽样数据中，其最大值为157，最小值为76，若确定组距为10，则这80个数据应分成组．

查看试题解析
13. 如图，△ABC中，∠ACB=90°，CD⊥AB于D，则点A到直线BC的距离是线段的长．

查看试题解析
14. 若关于x、y的二元一次方程组 ${\begin{array}{l} 2 x + m y = 5 \\ x - n y = 4 \end{array}$ 的解是 ${\begin{array}{l} x = 3 \\ y = 5 \end{array}$ ，则关于s、t的二元一次方程组 ${\begin{array}{l} 2 (s + t) + m (s - t) = 5 \\ (s + t) - n (s - t) = 4 \end{array}$ 的解是．

查看试题解析
15. 如图所示，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若B（m，3），C（n，-5），A（4，0），则AD•BC= ．

查看试题解析
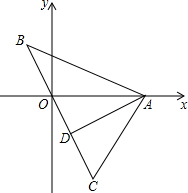16. 已知不等式组 ${\begin{array}{l} 1 < x < 5 \\ a < x < a + 3 \end{array}$ 的解集为a＜x＜5．则a的范围是．

查看试题解析

三、解答题

17.

(1)、计算： $- 1^{2} + | \sqrt{3} - 2 | - \sqrt[3]{27} \times (- \frac{1}{9})$ ；

(2)、解二元一次方程 ${\begin{array}{l} 2 x + 3 y = 12 \\ 3 x + 4 y = 17 \end{array}$ ．

查看试题解析
18.

(1)、解不等式6-2（x+1）≤3（x-2）．

(2)、解不等式组 ${\begin{array}{l} x ⩾ 3 (x - 2) + 4 \\ \frac{2 x}{5} - 1 < \frac{x - 1}{2} \end{array}$ ，并写出该不等式组的整数解．

查看试题解析
19. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为（-4，5），（-1，3）．

(1)、请在网格平面内作出平面直角坐标系；

(2)、将△ABC平移至△DEF，使得A、B、C的对应点依次是D、E、F，已知D（2，3），请在网格中作出△DEF；

(3)、若Q（a，b）是△DEF内一点，则△ABC内点Q的对应点点P的坐标是（用a、b表示）

查看试题解析
20. 为丰富学生课余生活，我校准备开设兴趣课堂．为了了解学生对绘画、书法、舞蹈、乐器这四个兴趣小组的喜爱情况，在全校进行随机抽样调查，并根据收集的数据绘制了下面两幅统计图（信息尚不完整），请根据图中提供的信息，解答下面的问题：

(1)、此次共调查了多少名同学？

(2)、将条形图补充完整，并计算扇形统计图中乐器部分的圆心角的度数；

(3)、如果我校共有1000名学生参加这4个课外兴趣小组，而每个教师最多只能辅导本组的25名学生，估计书法兴趣小组至少需要准备多少名教师？

查看试题解析
21. 某校6名教师和234名学生外出参加集体活动，学校准备租用45座大车和30座小车若干辆．已知租用1辆大车、2辆小车的租车费用是1000元，租用2辆大车、1辆小车的租车费用是100元．

(1)、每辆大车、小车的租车费用各是多少元？

(2)、学校要求每辆车上至少要有一名教师，且租车总费用不超过2300元，请问有几种符合条件的租车方案？哪种租车方案最省钱？

查看试题解析
22. △AOB中，∠AOB=90°，以顶点O为原点，分别以OA、OB所在直线为x轴、y轴建立平面直角坐标系（如图），点A（a，0），B（0，b）满足 $\sqrt{b - 2 a}$ +|a-2|=0

(1)、点A的坐标为；点B的坐标为．

(2)、如图①，已知坐标轴上有两动点D、E同时出发，点D从A点出发沿x轴负方向以每秒1个单位长度的速度匀速移动，点E从O点出发以每秒2个单位长度的速度沿y轴正方向移动，点E到达B点时运动结束，AB的中点C的坐标是（1，2），设运动时间为t（t＞0）秒，问：是否存在这样的t，使S△OCD=S△OCE？若存在，请求出t的值：若不存在，请说明理由．

(3)、如图②，点F是线段AB上一点，满足∠FOA=∠FAO，点G是第二象限中一点，连OG使得∠BOG=∠BOF，点P是线段OB上一动点，连AP交OF于点Q，当点P在线段OB上运动的过程中， $k = \frac{∠ O Q A + ∠ B A P}{∠ O P A}$ 的值是否会发生变化？若不变，请求出k的值；若变化，请说明理由．

查看试题解析