安徽省2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-05-25 类型:期末考试
一、选择题
-
1. 25的算术平方根是( )A、5 B、 C、-5 D、±52. 如图,同位角是( )
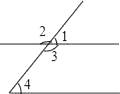 A、∠1和∠2 B、∠3和∠4 C、∠2和∠4 D、∠1和∠43.
A、∠1和∠2 B、∠3和∠4 C、∠2和∠4 D、∠1和∠43.如图天平右盘中的每个砝码的质量都是1g,则物体A的质量m(g)的取值范围在数轴上可表示为( )
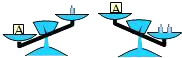 A、
A、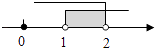 B、
B、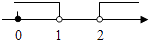 C、
C、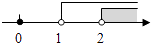 D、
D、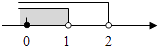 4. 如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是( )
4. 如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是( )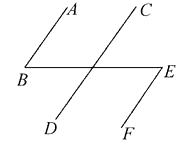 A、平行 B、相交 C、垂直 D、不能确定5. 由x<y得到ax>ay的条件是( )A、a≥0 B、a≤0 C、a>0 D、a<06. 若(x+5)(2x-n)=2x2+mx-15,则( )A、m=-7,n=3 B、m=7,n=-3 C、m=-7,n=-3 D、m=7,n=37. 计算-a2÷( )•( )的结果是( )A、1 B、 C、- D、-8. 设 ,则a、b的大小关系是( )A、a=b B、a>b C、a<b D、以上三种都不对9. 一个长方形的长增加50%,宽减少50%,那么长方形的面积( )A、不变 B、增加50% C、减少25% D、不能确定10. 有游客m人,如果每n个人住一个房间,结果还有一个人无房住,则客房的间数为( )A、 B、 C、 D、
A、平行 B、相交 C、垂直 D、不能确定5. 由x<y得到ax>ay的条件是( )A、a≥0 B、a≤0 C、a>0 D、a<06. 若(x+5)(2x-n)=2x2+mx-15,则( )A、m=-7,n=3 B、m=7,n=-3 C、m=-7,n=-3 D、m=7,n=37. 计算-a2÷( )•( )的结果是( )A、1 B、 C、- D、-8. 设 ,则a、b的大小关系是( )A、a=b B、a>b C、a<b D、以上三种都不对9. 一个长方形的长增加50%,宽减少50%,那么长方形的面积( )A、不变 B、增加50% C、减少25% D、不能确定10. 有游客m人,如果每n个人住一个房间,结果还有一个人无房住,则客房的间数为( )A、 B、 C、 D、二、填空题
-
11. 的立方根是 .12. 如图所示,直线AB,CD相交于点O,已知∠AOC=70°,OE平分∠BOD,则∠EOD= .
 13. 观察下列顺序排列的等式:9×0+1=1,9×1+2=11,9×2+3=21,9×3+4=31,9×4+5=41,…
13. 观察下列顺序排列的等式:9×0+1=1,9×1+2=11,9×2+3=21,9×3+4=31,9×4+5=41,…猜想第n个等式(n为正整数)应为9(n-1)+n= .
14. 若关于x的不等式2x-a≤0只有六个正整数解,则a应满足 .三、计算题
-
15. 解不等式组 .16. 先化简,再求值: ÷(x-2- ),其中x=3.17. 北京奥运会开幕前,某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68 000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)、该商场两次共购进这种运动服多少套?(2)、如果这两批运动服每套的售价相同,且全部售完后总利润率不低于20%,那么每套售价至少是多少元?(利润率= ×100%)
四、解答题
-
18. 解方程: .19. 根据提示,完成推理:
已知,AC⊥AB,EF⊥BC,AD⊥BC,∠1=∠2,请问AC⊥DG吗?请写出推理过程
解:AC⊥DG,理由如下:
∵EF⊥BC,AD⊥BC,
∴AD∥EF.
∴∠2=∠3.
……
请完成以上推理过程.
 20.
20. (1)、请把下面的小船图案先向上平移3格,再向右平移4格,画出平移后的小船的图形;(2)、若方格是由边长为1的小正方形构成的,试求小船所占的面积.21. 完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
(1)、请把下面的小船图案先向上平移3格,再向右平移4格,画出平移后的小船的图形;(2)、若方格是由边长为1的小正方形构成的,试求小船所占的面积.21. 完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD求证:∠EGF=90°
证明:∵HG∥AB(已知)
∴∠1=∠3
又∵HG∥CD(已知)
∴∠2=∠4
∵AB∥CD(已知)
∴∠BEF+=180°
又∵EG平分∠BEF(已知)
∴∠1= ∠
又∵FG平分∠EFD(已知)
∴∠2= ∠
∴∠1+∠2= ()
∴∠1+∠2=90°
∴∠3+∠4=90°即∠EGF=90°.
 22. 雅美服装厂有A种布料70m,B种布料52米.现计划用这两种布料生产M、N两种型号的时装共80套,已知做一套M型号的时装共需A种布料0.6m,B种布料0.9m;做一套N型号的时装需要A种布料1.1m,B种布料0.4m.(1)、设生产x套M型号的时装,写出x应满足的不等式组;(2)、有哪几种正确的生产方案?请你帮助设计出来.23. 直线AB∥CD,点P在其所在平面上,且不在直线AB,CD,AC上,设∠PAB=α,∠PCD=β,∠APC=γ(α,β,γ,均不大于180°,且不小于0°)
22. 雅美服装厂有A种布料70m,B种布料52米.现计划用这两种布料生产M、N两种型号的时装共80套,已知做一套M型号的时装共需A种布料0.6m,B种布料0.9m;做一套N型号的时装需要A种布料1.1m,B种布料0.4m.(1)、设生产x套M型号的时装,写出x应满足的不等式组;(2)、有哪几种正确的生产方案?请你帮助设计出来.23. 直线AB∥CD,点P在其所在平面上,且不在直线AB,CD,AC上,设∠PAB=α,∠PCD=β,∠APC=γ(α,β,γ,均不大于180°,且不小于0°) (1)、如图1,当点P在两条平行直线AB,CD之间、直线AC的右边时试确定α,β,γ的数量关系;(2)、如图2,当点P在直线AB的上面、直线AC的右边时试确定α,β,γ的数量关系;(3)、α,β,γ的数量关系除了上面的两种关系之外,还有其他的数量关系,请写出这些.
(1)、如图1,当点P在两条平行直线AB,CD之间、直线AC的右边时试确定α,β,γ的数量关系;(2)、如图2,当点P在直线AB的上面、直线AC的右边时试确定α,β,γ的数量关系;(3)、α,β,γ的数量关系除了上面的两种关系之外,还有其他的数量关系,请写出这些.