安徽省合肥五十中天鹅湖集团2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2020-05-25 类型：期中考试

进入出卷网下载

一、选择题

1. 下列实数中是无理数的是（　　）

A、 $\sqrt{3}$ B、（π﹣1）⁰ C、2 D、 $\sqrt{4}$

查看试题解析
2. 成人体内成熟的细胞的平均直径一般为0.000000725m，可以用科学记数法表示为（　　）

A、7.25×10⁶m B、7.25×10⁷m C、7.25×10^﹣6m D、7.25×10^﹣7m

查看试题解析
3. $\sqrt{5}$ 介于下列哪两个整数之间（）

A、0与1 B、1与2 C、2与3 D、3与4

查看试题解析
4. 若a＜b，则下列不等式中一定成立的是（　　）

A、a+3＜b+2 B、2﹣a＜2﹣b C、ac＜bc D、a﹣8＜b﹣7

查看试题解析
5. 计算（x+1）（x²+1）（x﹣1）的结果正确的是（　　）

A、x⁴+1 B、（x+1）⁴ C、x⁴﹣1 D、（x﹣1）⁴

查看试题解析
6. 如果关于x的不等式ax＞a的解集为x＜1，则a的取值范围是（　　）

A、a＞0 B、a＜0 C、a＜1 D、a＞1

查看试题解析
7. 若x²﹣mx+16是一个完全平方式，则m的值为（　　）

A、8 B、±8 C、±4 D、﹣8

查看试题解析
8. 一个三角形的面积为（x³y）² ，它的一条边长为（2xy）² ，那么这条边上的高为（　　）

A、 $\frac{1}{2} x^{4}$ B、 $\frac{1}{4} x^{4}$ C、 $\frac{1}{2} x^{4} y$ D、 $\frac{1}{2} x^{2}$

查看试题解析
9. 数轴上A、B两点表示的数分别为﹣2和 $\sqrt{2}$ ，数轴上点C在点A的左侧，到点A的距离等于点B到点A的距离，则点C所表示的数为（　　）

A、﹣3+ $\sqrt{2}$ B、﹣3﹣ $\sqrt{2}$ C、﹣4+ $\sqrt{2}$ D、﹣4﹣ $\sqrt{2}$

查看试题解析
10. 关于x的不等式组 ${\begin{cases} x - 2 > 2 b \\ 2 x - 1 < 3 b \end{cases}$ 无解，则常数b的取值范围是（）

A、b＞﹣3 B、b≥﹣3 C、b≤﹣3 D、b＜﹣3

查看试题解析

二、填空题（共6小题，满分18分）

11. 计算： $\sqrt{16}$ = ．

查看试题解析
12. 不等式3（x﹣1）≤x+2的正整数解是．

查看试题解析
13. 计算：1﹣ ${(- \frac{5}{7})}^{2019}$ × ${(1 \frac{2}{7})}^{2018}$ ＝．

查看试题解析
14. 已知，x+y＝2，xy＝﹣5，则（x﹣y）²＝．

查看试题解析
15. 已知3^a＝5，3^b＝2，则3^2a^﹣3b＝．

查看试题解析
16. 2019年4月4日，中国国际女足锦标赛半决赛在武汉进行，这场由中国队迎战俄罗斯队的比赛牵动着众多足球爱好者的心．在未开始检票入场前，已有1200名足球爱好者排队等待入场．假设检票开始后，每分钟赶来的足球爱好者人数是固定的，1个检票口每分钟可以进入40人．如果4个检票口同时检票，15分钟后排队现象消失；如果7个检票口同时检票，分钟后排队现象消失．

查看试题解析

三、解答题

17. 计算：

(1)、 $^{3} \sqrt{- 8}$ ﹣ ${(2 - π)}^{0}$ + ${(\frac{1}{2})}^{- 2}$

(2)、 $\sqrt{4}$ ﹣ $\sqrt{2}$ +|1﹣ $\sqrt{3}$ |（精确到0.01）

查看试题解析
18. 解不等式组 ${\begin{cases} 2 x + 5 < 3 (x + 2) \\ \frac{x + 1}{3} \geq \frac{x}{2} \end{cases}$ ，并把它的解集在数轴上表示．

查看试题解析
19. 先化简，再求值：（x﹣y）²﹣（x+y）（x﹣3y）﹣3y² ．其中|x﹣1|+|y+2|＝0．

查看试题解析
20. 观察下列等式：
①1×3＝3：②3×5＝15：③5×7＝35；④7×9＝63；…

(1)、写出第n个等式（n为正整数）

(2)、是否存在正整数n，使等式右边等于2499，如果存在，求出n；若不存在，请说明理由

查看试题解析
21. 乘法公式的探究及应用．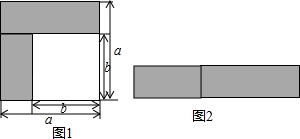

(1)、如图1，阴影部分的面积是（写成平方差的形式）；

(2)、如图2，若将阴影部分裁剪后重新拼成一个长方形，它的宽是长是，面积可表示为（写成多项式乘法的形式）．

(3)、运用以上得到的公式，计算：（x﹣2y+3z）（x+2y﹣3z）

查看试题解析
22. 某造纸企业为了更好地处理污水问题，决定购买10台新型污水处理设备．甲、乙两种型号的设备可选，其中每台的价格，月处理污水量如表：

A型

B型

价格（万元/）

10

8

处理污水量（吨/月）

180

150

(1)、经预算：该企业购买污水处理设备的资金不超过85万元，你认为该企业有哪几种购买方案．

(2)、在（1）的条件下，若每月需要处理的污水不低于1530吨，为了节约资金，请你为该企业设计一种最省钱的购买方案．

查看试题解析

	A型	B型
价格（万元/）	10	8
处理污水量（吨/月）	180	150