安徽省宿州市埇桥区集团校2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-25 类型:期末考试
一、选择题
-
1. 下列图案中,不是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 若 ,下列不等式一定成立的是A、 B、 C、 D、3. 下列各式从左到右的变形中,是因式分解的为( ).A、 B、 C、 D、4. 不等式组 有 个整数解.A、2 B、3 C、4 D、55. 若分式 的值为零,则 等于A、2 B、 C、 D、06. 如图,在 中, , , ,将 沿 向右平移得到 .若四边形 的面积等于8,则平移距离等于
2. 若 ,下列不等式一定成立的是A、 B、 C、 D、3. 下列各式从左到右的变形中,是因式分解的为( ).A、 B、 C、 D、4. 不等式组 有 个整数解.A、2 B、3 C、4 D、55. 若分式 的值为零,则 等于A、2 B、 C、 D、06. 如图,在 中, , , ,将 沿 向右平移得到 .若四边形 的面积等于8,则平移距离等于 A、2 B、4 C、8 D、167. 如图,平行四边形 中, 的平分线 交 于 , , ,则 的长
A、2 B、4 C、8 D、167. 如图,平行四边形 中, 的平分线 交 于 , , ,则 的长 A、1 B、1.5 C、2 D、38. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需的时间与原计划生产450台机器所需时间相同.设原计划每天生产 台机器,则可列方程为A、 B、 C、 D、9. 如图,在 中, , , 垂直平分斜边 ,交 于 , 是垂足,连接 ,若 ,则 的长是
A、1 B、1.5 C、2 D、38. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需的时间与原计划生产450台机器所需时间相同.设原计划每天生产 台机器,则可列方程为A、 B、 C、 D、9. 如图,在 中, , , 垂直平分斜边 ,交 于 , 是垂足,连接 ,若 ,则 的长是 A、 B、4 C、 D、610. 如图,四边形 中, , , ,点 , 分别为线段 , 上的动点(含端点,但点 不与点 重合),点 , 分别为 , 的中点,则 长度的最大值为
A、 B、4 C、 D、610. 如图,四边形 中, , , ,点 , 分别为线段 , 上的动点(含端点,但点 不与点 重合),点 , 分别为 , 的中点,则 长度的最大值为 A、8 B、6 C、4 D、5
A、8 B、6 C、4 D、5二、填空题
-
11. 已知 , 是二元一次方程组 的解,则代数式 的值为 .12. 若关于x的分式方程 + =2有增根,则m的值为 .13. 如图, 是等腰直角三角形, 是斜边,将 绕点 逆时针旋转后,能与 重合,如果 ,那么 .
 14. 有一张一个角为 ,最小变长为4的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是 .
14. 有一张一个角为 ,最小变长为4的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,所得四边形的周长是 .
三、解答题
-
15. 分解因式: .16. 分解因式:
四、解答题
-
17. 解不等式:18. 先化简,再求值 ,其中 .
五、解答题
-
19. 如图,方格纸中每个小正方形的边长都是1个单位长度, 的三个顶点 , , .
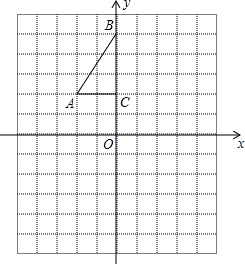 (1)、将 以点 为旋转中心旋转 ,得到△ ,请画出△ 的图形;(2)、平移 ,使点 的对应点 坐标为 ,请画出平移后对应的△ 的图形;(3)、若将△ 绕某一点旋转 可得到△ ,请直接写出旋转中心的坐标.20. 高铁的开通给滕州人民出行带来极大的方便,从滕州到北京相距 ,现在乘高铁列车比以前乘特快列车少用 ,已知高铁列车的平均速度是特快列车的2.8倍,求高铁列车的平均行驶速度.
(1)、将 以点 为旋转中心旋转 ,得到△ ,请画出△ 的图形;(2)、平移 ,使点 的对应点 坐标为 ,请画出平移后对应的△ 的图形;(3)、若将△ 绕某一点旋转 可得到△ ,请直接写出旋转中心的坐标.20. 高铁的开通给滕州人民出行带来极大的方便,从滕州到北京相距 ,现在乘高铁列车比以前乘特快列车少用 ,已知高铁列车的平均速度是特快列车的2.8倍,求高铁列车的平均行驶速度.
六、解答题(本题满分8分)
-
21. 如图,平行四边形 中,点 是 与 的交点,过点 的直线与 , 的延长线分别交于点 , .
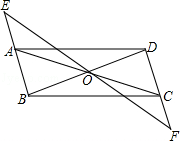 (1)、求证: ;(2)、连接 , ,求证:四边形 是平行四边形.
(1)、求证: ;(2)、连接 , ,求证:四边形 是平行四边形.七、解答题(本题满分8分)
