安徽省铜陵市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-05-25 类型：期末考试

进入出卷网下载

一、选择题

1. 下列计算不正确的是（　　）

A、 $\sqrt{8} - \sqrt{2}$ = $\sqrt{2}$ B、 $\sqrt{8}$ ÷2= $\sqrt{2}$ C、3 $+ 2 \sqrt{2}$ =5 $\sqrt{2}$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$

查看试题解析
2. 下列二次根式中，最简二次根式是（　　）

A、 $\sqrt{a^{2} + b^{2}}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{8}$ D、 $\sqrt{a^{2} b}$

查看试题解析
3. 在Rt△ABC中，∠ACB=90°，AB=3，则AB²+BC²+AC²=（　　）

A、9 B、18 C、20 D、24

查看试题解析
4. 某班抽取6名同学进行体育达标测试，成绩如下：80，90，75，80，75，80．下列关于对这组数据的描述不正确的是（　　）

A、众数是80 B、平均数是80 C、中位数是75 D、极差是15

查看试题解析
5. 一个四边形，对于下列条件：①一组对边平行，一组对角相等；②一组对边平行，一条对角线被另一条对角线平分；③一组对边相等，一条对角线被另一条对角线平分；④两组对角的平分线分别平行，不能判定为平行四边形的是（）

A、① B、② C、③ D、④

查看试题解析
6. 若一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的方差是3，则2x₁-3，2x₂-3，2x₃-3，2x₄-3，2x₅-3的方差是（　　）

A、3 B、6 C、9 D、12

查看试题解析
7. 一次函数y=kx+b与y=bx+k的图象在同一坐标系中的图象大致是（　　）

A、 B、 C、 D、

查看试题解析
8. 已知锐角三角形的边长是2，3，x，那么第三边x的取值范围是( )

A、1＜x＜ $\sqrt{5}$ B、 $\sqrt{5} < x < \sqrt{13}$ C、 $\sqrt{13}$ ＜x＜5 D、 $\sqrt{5}$ ＜x＜ $\sqrt{15}$

查看试题解析
9. 如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，则MN的长度为（）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、3

查看试题解析
10. 如图，直线y=x+1与y轴交于点A₁ ，依次作正方形A₁B₁C₁O、正方形A₂B₂C₂C₁、…、正方形A_nB_nC_nC_n-1 ，使得点A₁、A₂、…，A_n在直线x+1上，点C₁、C₂、…，C_n在x轴上，则点B_n的坐标是（　　）

A、（2ⁿ-1，2^n-1） B、（2^n-1+1，2^n-1） C、（2n-1，2n-1） D、（2n-1，n）

查看试题解析

二、填空题

11. 若二次根式 $\sqrt{x + 1}$ 有意义，则x的取值范围是．

查看试题解析
12. 已知一组数据10，10，x，8的众数与它的平均数相等，则这组数的中位数是．

查看试题解析
13. 某市在旧城改造中，计划在市内一块如图所示三角形空地上种植草皮以美化环境，已知这种草皮每平方米售价a元，则购买这种草皮至少需要．

查看试题解析
14. 如图，长方体的底面边长分别为1cm 和3cm，高为6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要cm．

查看试题解析
15. 若三角形的周长为28cm，则它的三条中位线组成的三角形的周长是．

查看试题解析
16. A、B两城相距600千米，甲、乙两车同时从A城出发驶向B城，甲车到达B城后立即返回，返回途中与乙车相遇．如图是它们离A城的距离y（km）与行驶时间x（h）之间的函数图象．当它们行驶7（h）时，两车相遇，则乙车速度的速度为．

查看试题解析

三、解答题

17.

(1)、 $\sqrt{48}$ ÷ $\sqrt{3}$ - $\frac{1}{2}$ × $\sqrt{12}$ + $\sqrt{24}$

(2)、 $\frac{2}{3} \sqrt{27 a^{2}}$ - $a^{2} \sqrt{\frac{3}{a}}$ +6a $\sqrt{\frac{a}{3}}$

查看试题解析
18. 如图，在△ABC中，AC=9，AB=12，BC=15，P为BC边上一动点，PG⊥AC于点G，PH⊥AB于点H．

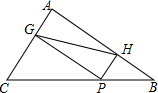(1)、求证：四边形AGPH是矩形；

(2)、在点P的运动过程中，GH的长度是否存在最小值？若存在，请求出最小值，若不存在，请说明理由．

查看试题解析
19.
某市团委举办“我的中国梦”为主题的知识竞赛，甲、乙两所学校参赛人数相等，比赛结束后，发现学生成绩分别为70分，80分，90分，100分，并根据统计数据绘制了如下不完整的统计图表：
乙校成绩统计表
分数（分）
人数（人）
70
7
80

90
1
100
8

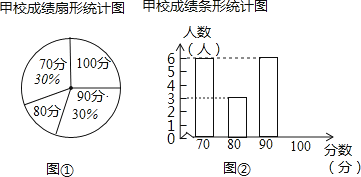(1)、在图①中，“80分”所在扇形的圆心角度数为；

(2)、请你将图②补充完整；

(3)、求乙校成绩的平均分；

(4)、经计算知S_甲²=135，S_乙²=175，请你根据这两个数据，对甲、乙两校成绩作出合理评价．

查看试题解析
20. 如图，直线y=- $\frac{4}{3}$ x+8与x轴、y轴分别相交于点A、B，设M是OB上一点，若将△ABM沿AM折叠，使点B恰好落在x轴上的点B′处．求：

(1)、点B′的坐标；

(2)、直线AM所对应的函数关系式．

查看试题解析
21. 某项工程由甲乙两队分别单独完成，则甲队用时是乙队的1.5倍；若甲乙两队合作，则需12天完成，请问：

(1)、甲，乙两队单独完成各需多少天；

(2)、若施工方案是甲队先单独施工x天，剩下工程甲乙两队合作完成，若甲队施工费用为每天1.5万元，乙队施工费为每天3.5万元．求施工总费用y（万元）关于施工时间x（天）的函数关系式；

(3)、在（2）的方案下，若施工期定为15～18天内完成（含15和18天），如何安排施工方案使费用最少，最少费用为多少万元？

查看试题解析
22. 如图，在菱形ABCD中，∠DAB=60°，点E，F将对角线AC三等分，且AC=6，连接DE，DF，BE，BF．

(1)、求证：四边形DEBF为菱形；

(2)、求菱形DEBF的面积；

(3)、若P是菱形ABCD的边上的点，则满足PE+PF= $\sqrt{13}$ 的点P的个数是个．

查看试题解析

分数（分）	人数（人）
70	7
80
90	1
100	8