安徽省六安市舒城县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期：2020-05-25 类型：期末考试
一、选择题
-
1. 下列不是 同类二次根式的是（ ）A、 B、 C、 D、2. 方程x2-2x=0的解是（ ）A、x=2 B、x1= ，x2=0 C、x1=2，x2=0 D、x=03. 小宇同学投擦10次实心球的成绩如表所示：
成绩（m）
11.8
11.9
12
12.1
12.2
频数
2
2
2
3
1
由上表可知小宇同学投掷10次实心球成绩的众数与中位数分别是（ ）
A、12m，11.9m B、12m，12.1m C、12.1m，11.9m D、12.1m，12m4. 如图，在四边形ABCD中，对角线AC，BD相交于点O，AO=CO，BO=DO．添加下列条件，不能判定四边形ABCD是菱形的是（ ）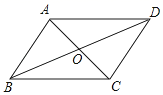
A、AB=AD B、AC=BD C、AC⊥BD D、∠ABO=∠CBO5. 已知关于x的方程x2-kx+6=0有两个实数根，则k的值不可能是（ ）A、5 B、-8 C、2 D、46. 在△ABC中，AC=9，BC=12，AB=15，则AB边上的高是（ ）A、 B、 C、 D、7. 在同一时期分别从甲、乙、丙，丁四种小麦中随机抽取部分麦苗，获得苗高（单位：cm）的平均数与方差为： = =13cm， = =15cm；S甲2=S丁2=3.6cm2 ， S乙2=S丙2=6.3cm2 ， 则麦苗又高又齐的是（ ）A、甲 B、乙 C、丙 D、丁8. 我县某贫围户2016年的家庭年收入为4000元，由于党的扶贫政策的落实，2017、2018年家庭年收入增加到共15000元，设平均每年的增长率为x，可得方程（ ）A、4000（1+x）2=15000 B、4000+4000（1+x）+4000（1+x）2=15000 C、4000（1+x）+4000（1+x）2=15000 D、4000+4000（1+x）2=150009. 如图所示，在菱形ABCD中，E、F分别是AB、AC的中点，如果EF=2，那么菱形ABCD的周长是（ ）
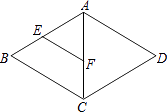A、4 B、8 C、12 D、1610. 如图，平行四边形ABCD对角线AC、BD交于点O，∠ADB=20°，∠ACB=50°，过点O的直线交AD于点E，交BC于点F当点E从点A向点D移动过程中（点E与点A、点D不重合），四边形AFCE的形状变化依次是（ ）
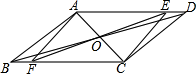A、平行四边形→矩形→平行四边形→菱形→平行四边形 B、平行四边形→矩形→平行四边形→正方形→平行四边形 C、平行四边形→菱形→平行四边形→矩形→平行四边形 D、平行四边形→矩形→菱形→正方形→平行四边形二、填空题
-
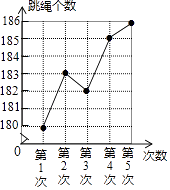
11. 函数y= 自变量x的取值范围是 ．12. 某同学在体育训练中统计了自己五次“1分钟跳绳”成绩，并绘制了如图所示的折线统计图，这五次“1分钟跳绳”成绩的中位数是个．
13. 一个正n边形的每个内角都是108°，则n= ．14. 在Rt△ABC中，∠C=90°，AC=3，BC=5．作一边的垂直平分线交另一边于点D，则CD的长是 ．15. 如图，在矩形ABCD中，AB=8，AD=3，点E是CD的中点，连接AE，将△ADE沿直线AE折叠，使点D落在点F处，则线段CF的长度是 ．
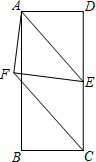
三、解答题
-
16. 计算：（ -2）（ +1）17. 在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．
(1)、求证：△ABE≌△ADF；(2)、试判断四边形AECF的形状，并说明理由．18. 某校为加强学生安全意识，组织了全校1500名学生参加安全知识竞赛，从中抽取了部分学生成绩（得分取正整数，满分100分）进行统计，请根据尚为完成的频率和频数分布直方图，解答下列问题：分数段
频数
频率
50.5～60.5
16
0.08
60.5～70.5
40
0.2
70.5～80.5
50
0.25
80.5～90.5
m
0.35
90.5～100.5
24
n
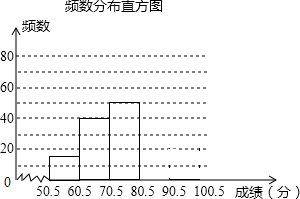(1)、这次抽取了名学生的竞赛成绩进行统计，其中m= ， n=；(2)、补全频数分布直方图；(3)、若成绩在70分以下（含70分）的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有多少人？19. 如图，将正方形OEFG放在平面直角坐标系中，O是坐标原点，点F的坐标为（-1，5），求点E的坐标．
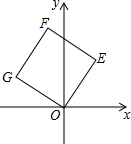20. 如图1，P是菱形ABCD对角线AC上的一点，点E在BC的延长线上，且PE=PB．
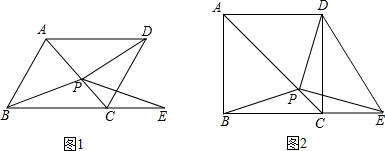(1)、求证：PD=PE；(2)、求证：∠DPE=∠ABC；(3)、如图2，当四边形ABCD为正方形时，连接DE，试探究线段DE与线段BP的数量关系，并说明理由．四、计算题