安徽省六安市寿县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-25 类型:期末考试
一、选择题
-
1. 当 有意义时,a的取值范围是( )A、a≥2 B、a>2 C、a≠2 D、a≠-22. 在某市举办的垂钓比赛上,5名垂钓爱好者参加了比赛,比赛结束后,统计了他们各自的钓鱼条数,成绩如下:4,5,10,6,10.则这组数据的中位数是( )A、5 B、6 C、7 D、103. 下列各式计算正确的是( )A、 B、 C、 D、4. 已知2是关于x的方程x2-2ax+4=0的一个解,则a的值是( )A、1 B、2 C、3 D、45. 数据-2,-1,0,1,2的方差是( )A、 B、2 C、1 D、2.56. 将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有( )
A、1种 B、2种 C、4种 D、无数种7. 下列说法中不正确的是( )A、一组对边平行且一组对角相等的四边形是平行四边形 B、每组邻边都相等的四边形是菱形 C、四个角都相等的四边形是矩形 D、对角线互相垂直平分的四边形是正方形8. 已知一元二次方程x2-2x-1=0的两根分别为x1 , x2 , 则 + 的值为( )A、2 B、-1 C、 D、-29. 如图,将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起,其中点A′与点A重合,点C′落在边AB上,连接B′C.若∠ACB=∠AC′B′=90°,AC=BC=3,则B′C的长为( ) A、3 B、6 C、3 D、10. 在△ABC中,AB=BC=2,O是线段AB的中点,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为( )A、1, ,7 B、1, , C、1, D、1,3,
A、3 B、6 C、3 D、10. 在△ABC中,AB=BC=2,O是线段AB的中点,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为( )A、1, ,7 B、1, , C、1, D、1,3,二、填空题
-
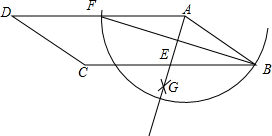
11. 正六边形的每个内角等于°.12. 若关于x的一元二次方程(k-1)x2+4x+1=0有实数根,则k的取值范围是13. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为 .
 14. 如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=时,四边形MENF是正方形.
14. 如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是边BM、CM的中点,当AB:AD=时,四边形MENF是正方形.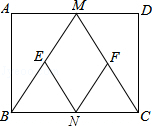
三、计算题
-
15. 计算: .16. 解方程:x(x-3)=4.
四、解答题(本大题共 7 小题,共 74 分)
-
17.
如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点四边形,使P在四边形内部(不包括边界上),且P到四边形的两个顶点的距离相等.
 (1)、在图甲中画出一个▱ABCD.(2)、在图乙中画出一个四边形ABCD,使∠D=90°,且∠A≠90°.(注:图甲、乙在答题纸上)18. 如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求:
(1)、在图甲中画出一个▱ABCD.(2)、在图乙中画出一个四边形ABCD,使∠D=90°,且∠A≠90°.(注:图甲、乙在答题纸上)18. 如图,一次函数y=kx+b的图象经过(2,4)、(0,2)两点,与x轴相交于点C.求: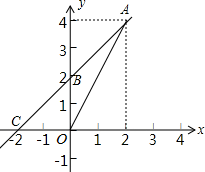 (1)、此一次函数的解析式;(2)、△AOC的面积.19. 若关于x的一元二次方程x2-2(2-k)x+k2+12=0有实数根α、β.(1)、求实数k的取值范围;(2)、设 ,求t的最小值.20. 某校举行了“文明在我身边”摄影比赛,已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分步赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
(1)、此一次函数的解析式;(2)、△AOC的面积.19. 若关于x的一元二次方程x2-2(2-k)x+k2+12=0有实数根α、β.(1)、求实数k的取值范围;(2)、设 ,求t的最小值.20. 某校举行了“文明在我身边”摄影比赛,已知每幅参赛作品成绩记为x分(60≤x≤100).校方从600幅参赛作品中随机抽取了部分步赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.“文明在我身边”摄影比赛成绩统计表
分数段
频数
频率
60≤x<70
18
0.36
70≤x<80
17
c
80≤x<90
a
0.24
90≤x≤100
b
0.06
合计
1

根据以上信息解答下列问题:
(1)、统计表中a= , b= , c= .(2)、补全数分布直方图;(3)、若80分以上的作品将被组织展评,试估计全校被展评作品数量是多少?21. 矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
求证:
(1)、四边形AFCE是平行四边形;(2)、EG=FH.22. 随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.(1)、该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;(2)、若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为t.①若该养老中心建成后可提供养老床位200个,求t的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
23. 问题背景如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
类比探究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)
 (1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.(2)、△DEF是否为正三角形?请说明理由.(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
(1)、△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.(2)、△DEF是否为正三角形?请说明理由.(3)、进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.