安徽省淮南市谢家集区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-05-25 类型：期末考试

进入出卷网下载

1. 下列二次根式中，化简后能与 $\sqrt{2}$ 合并的是 $($ 　　 $)$

A、 $\sqrt{4}$ B、 $\sqrt{8}$ C、 $\sqrt{12}$ D、 $\sqrt{24}$

查看试题解析
2. 下列四组线段中，可以构成直角三角形的是 $($ 　　 $)$

A、2，3，4 B、3，4，5 C、4，5，6 D、7，8，9

查看试题解析
3. 函数 $y = 2 x - 1$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 正方形、矩形、菱形都具有的特征是 $($ 　　 $)$

A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对角线平分一组对角

查看试题解析
5. 在端午节到来之前，儿童福利院对全体小朋友爱吃哪几种粽子作调查，以决定最终买哪种粽子．下面的调查数据中最值得关注的是（）

A、方差 B、平均数 C、中位数 D、众数

查看试题解析
6. 如图， $▱ A B C D$ 中， $∠ A = 100 °$ ， $∠ A B C$ 的平分线 $B E$ 交 $A D$ 于点 $E$ ，连接 $C E$ ，若 $B E = C E$ ，则 $∠ E C D$ 的度数为 $($ 　　 $)$

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析

7. 学习勾股定理时，数学兴趣小组设计并组织了“勾股定理的证明”的比赛，全班同学的比赛得分统计如表：

得分（分 $)$	60	70	80	90	100
人数（人 $)$	8	12	10	7	3

则得分的中位数和众数分别为 $($ 　　 $)$

A、75，70 B、75，80 C、80，70 D、80，80

8. 若 $A (x_{1}$ ， $y_{1})$ ， $B (x_{2}$ ， $y_{2})$ 是直线 $y = (m - 1) x + 2$ 上的两点，当 $x_{1} < x_{2}$ 时，有 $y_{1} > y_{2}$ ，则 $m$ 的取值范围是 $($ 　　 $)$

A、 $m > 1$ B、 $m < 1$ C、 $m \neq 1$ D、 $m < 0$

查看试题解析
9.
我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为（）

A、（ $\sqrt{3}$ ，1） B、（2，1） C、（1， $\sqrt{3}$ ） D、（2， $\sqrt{3}$ ）

查看试题解析
10. 已知一次函数 $y_{1} = x + a$ 与 $y_{2} = k x + b$ 的图象如图，则下列结论：① $k < 0$ ；② $a b > 0$ ；③关于 $x$ 的方程 $x + a = k x + b$ 的解为 $x = 2$ ；⑩当 $x ⩾ 2$ 时， $y_{1} ⩾ y_{2}$ ，其中正确的个数是 $($ 　　 $)$

A、1 B、2 C、3 D、4

查看试题解析

11. 函数 $y = \sqrt{2 - x}$ 中，自变量 $x$ 的取值范围是.

查看试题解析
12. 将直线 $y = 2 x + 3$ 向下平移4个单位，所得到的直线的解析式为．

查看试题解析
13. 如图，在四边形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于点 $O$ ， $A D / / B C$ ，请添加一个条件：，使四边形 $A B C D$ 为平行四边形（不添加任何辅助线）．

查看试题解析
14. 如图，数轴上点A表示的实数是．

查看试题解析
15. 在菱形 $A B C D$ 中， $∠ A = 60 °$ ，其周长为 $8 c m$ ，则菱形的面积为 $c m^{2}$ ．

查看试题解析
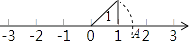16. 小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为85分，80分，90分，若依次按照 $2 : 3 : 5$ 的比例确定成绩，则小王的成绩是分．

查看试题解析
17. 已知直线 $y = k x + b$ 与直线 $y = - 2 x$ 平行且经过点 $(1, 2)$ ，则 $k + b =$ ．

查看试题解析
18. 如图，已知在矩形 $A B C D$ 中， $A B = 3$ ， $B C = 5$ ，沿着过矩形顶点的一条直线将 $∠ B$ 折叠，使点 $B$ 的对应点 $E$ 落在矩形的 $A D$ 边上，则折痕的长为．

查看试题解析

21. 我区举行“中华诵

\cdot

经典诵读”大赛，小学、中学组根据初赛成绩，各选出5名选手组成小学代表队和中学代表队参加市级决赛，两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图

根据以上信息，整理分析数据如下：

(1)、写出表格中

a

，

b

，

c

的值：

a =

，

b =

，

c =

．

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？

(3)、计算两队决赛成绩的方差，并判断哪一个代表队选手成绩较稳定．