安徽省合肥市瑶海区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-25 类型:期末考试
一、选择题
-
1. 下列计算中,正确的是( )A、 B、 C、 D、2. 一个多边形内角和是1080°,则这个多边形是( )A、六边形 B、七边形 C、八边形 D、九边形3. 用配方法解方程x2-2x-5=0时,原方程应变形为( )A、(x+1)2=6 B、(x-1)2=6 C、(x+2)2=9 D、(x-2)2=94. 下列各组数据为边的三角形中,是直角三角形的是( )A、8,15,16 B、5,12,15 C、2, , D、1,2,5. 观察下列一组数:1、1、 、 、 、2 ,____,按照这组数的规律横线上的数是( )A、2 B、 C、4 D、36. 我国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2017年年人均收入为3800美元,预计2019年年人均收入将达到5000美元,设2017年到2019年该地区居民年人均收入平均增长率为x,可列方程为( )A、3800(1+2x)=5000 B、3800(1+x2)=5000 C、3800(1+x)2=5000 D、3800+2x=50007. 如图,在▱ABCD中,AC与BD相交于点O,点E是边BC的中点,AB=4,则OE的长是( )
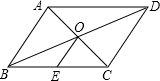 A、2 B、 C、1 D、8. 某学校在开展“节约每一滴水”的活动中,从九年级的500名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表所示
A、2 B、 C、1 D、8. 某学校在开展“节约每一滴水”的活动中,从九年级的500名同学中任选出10名同学汇报了各自家庭一个月的节水情况,将有关数据整理如下表所示节水量(单位:t)
0.5
1
1.5
2
同学数(人)
2
3
4
1
请你估计这500名同学的家庭一个月节约的水总量大约是( )
A、400t B、500t C、600t D、700t9. 如图,在△ABC中,点E,D,F分别在边AB、BC、CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )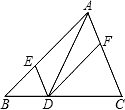 A、四边形AEDF是平行四边形 B、如果∠BAC=90°,那么四边形AEDF是矩形 C、如果AD平分∠BAC,那么四边形AEDF是菱形 D、如果AD⊥BC且AB=AC,那么四边形AEDF是正方形10. 如图,在矩形ABCD中,AB=2,AD=3,E是BC边上一点,将△ABE沿AE折叠,使点B落在点B′处,连接CB′,则CB′的最小值是( )
A、四边形AEDF是平行四边形 B、如果∠BAC=90°,那么四边形AEDF是矩形 C、如果AD平分∠BAC,那么四边形AEDF是菱形 D、如果AD⊥BC且AB=AC,那么四边形AEDF是正方形10. 如图,在矩形ABCD中,AB=2,AD=3,E是BC边上一点,将△ABE沿AE折叠,使点B落在点B′处,连接CB′,则CB′的最小值是( )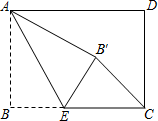 A、 -2 B、 +2 C、 -3 D、1
A、 -2 B、 +2 C、 -3 D、1二、填空题
-
11. 代数式 在实数范围内有意义,则x的取值范围是 .12. 若a是方程x2-2x-1=0的解,则代数式2a2-4a+2019的值为 .13. 如图,直角边分别为3,4的两个直角三角形如图摆放,M,N为斜边的中点,则线段MN的长为 .
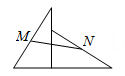 14. 在矩形ABCD中,AB=2,BC=6,直线EF经过对角线BD的中点O分别交边AD、BC与点E、F,点G、H分别是OB、OD的中点,当四边形EGFH为矩形时,则BF的长 .
14. 在矩形ABCD中,AB=2,BC=6,直线EF经过对角线BD的中点O分别交边AD、BC与点E、F,点G、H分别是OB、OD的中点,当四边形EGFH为矩形时,则BF的长 .三、解答题
-
15. 计算:(3 -2 + )÷2 .16. 解方程:(x-3)2+4x(x-3)=0.17. 如图,正方形网格中每个小正方形边长都是1,小正方形的顶点称为格点,在正方形网格中分别画出下列图形:
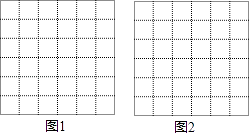 (1)、在网格中画出长为 的线段AB.(2)、在网格中画出一个腰长为 、面积为3的等腰△DEF.18. 已知关于x的一元二次方程x2-mx-3=0.(1)、求证:无论m取何实数,该方程总有两个不相等的实数根;(2)、若方程的一根为3,求另一个根.19. 如图1,一架云梯斜靠在一竖直的墙上,云梯的顶端距地面15米,梯子的长度比梯子底端离墙的距离大5米.
(1)、在网格中画出长为 的线段AB.(2)、在网格中画出一个腰长为 、面积为3的等腰△DEF.18. 已知关于x的一元二次方程x2-mx-3=0.(1)、求证:无论m取何实数,该方程总有两个不相等的实数根;(2)、若方程的一根为3,求另一个根.19. 如图1,一架云梯斜靠在一竖直的墙上,云梯的顶端距地面15米,梯子的长度比梯子底端离墙的距离大5米.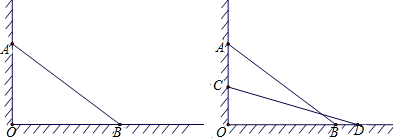 (1)、这个云梯的底端离墙多远?(2)、如图2,如果梯子的顶端下滑了8m,那么梯子的底部在水平方向滑动了多少米?20. 如图,平行四边形ABCD中,AE=CE.
(1)、这个云梯的底端离墙多远?(2)、如图2,如果梯子的顶端下滑了8m,那么梯子的底部在水平方向滑动了多少米?20. 如图,平行四边形ABCD中,AE=CE. (1)、用尺规或只用无刻度的直尺作出∠AEC的角平分线,保留作图痕迹,不需要写作法.(2)、设∠AEC的角平分线交边AD于点F,连接CF,求证:四边形AECF为菱形.21. 如图,有长为48米的篱笆,一面利用墙(墙的最大可用长度25米),围成中间隔有一道篱笆的长方形花圃ABCD.
(1)、用尺规或只用无刻度的直尺作出∠AEC的角平分线,保留作图痕迹,不需要写作法.(2)、设∠AEC的角平分线交边AD于点F,连接CF,求证:四边形AECF为菱形.21. 如图,有长为48米的篱笆,一面利用墙(墙的最大可用长度25米),围成中间隔有一道篱笆的长方形花圃ABCD.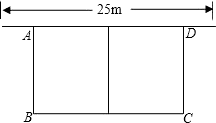 (1)、当AB的长是多少米时,围成长方形花圃ABCD的面积为180m2?(2)、能围成总面积为240m2的长方形花圃吗?说明理由.22. 通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:
(1)、当AB的长是多少米时,围成长方形花圃ABCD的面积为180m2?(2)、能围成总面积为240m2的长方形花圃吗?说明理由.22. 通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,先阅读再解决后面的问题:原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,求证:EF=BE+DF.
解题分析:由于AB=AD,我们可以延长CD到点G,使DG=BE,易得∠ABE=∠ADG=90°,可证△ABE≌△ADG
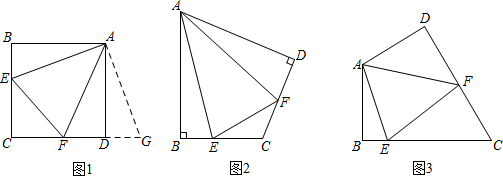
再证明△AFG≌△AFE,得EF=FG=DG+FD=BE+DF
(1)、如图2,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF= ∠BAD.求证:EF=BE+FD;
(2)、如图3,在四边形ABCD中,∠B=∠D=90°,∠BAD=120°,AB=AD=1,点E、F分别在四边形ABCD的边BC、CD上,且∠EAF=60°,求此时△CEF的周长.
四、计算题(本大题共 1 小题,共 12 分)
-
23. 某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上为合格,达到9分以上(含9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如下.
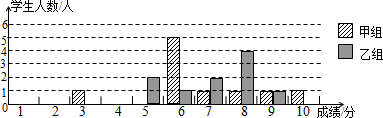 (1)、补充完成下列的成绩统计分析表:
(1)、补充完成下列的成绩统计分析表:组别
平均分
中位数
方差
合格率
优秀率
甲
6.7
3.41
90%
20%
乙
7.5
80%
10%
(2)、小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是组学生;(填“甲”或“乙”)(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.