安徽省合肥市蜀山区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-25 类型:期末考试
一、选择题
-
1. 下列根式中,不是最简二次根式的是( )A、 B、 C、 D、2. 下列各组数中,是勾股数的为( )A、 , , B、0.6,0.8,1.0 C、1,2,3 D、9,40,413. 若关于x的方程x2-bx+6=0的一根是x=2,则另一根是( )A、x=-3 B、x=-2 C、x=2 D、x=34. 如图,平行四边形ABCD中,AB=4,AD=5,AE平分∠BAD交BC边于点E,则CE的长为( )
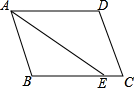 A、1 B、2 C、3 D、45. 我们知道正五边形不能进行平面镶嵌,若将三个全等的正五边形按如图所示拼接在一起,那么图中的∠1的度数是( )
A、1 B、2 C、3 D、45. 我们知道正五边形不能进行平面镶嵌,若将三个全等的正五边形按如图所示拼接在一起,那么图中的∠1的度数是( ) A、18° B、30° C、36° D、54°6. 若x- ,则x-y的值为( )A、2 B、1 C、0 D、-17. 质量检查员随机抽取甲、乙、丙、丁四台机器生产的20个乒乓球的直径(规格是直径4cm),整理后的平均数和方差如下表,那么这四台机器生产的乒乓球既标准又稳定的是( )
A、18° B、30° C、36° D、54°6. 若x- ,则x-y的值为( )A、2 B、1 C、0 D、-17. 质量检查员随机抽取甲、乙、丙、丁四台机器生产的20个乒乓球的直径(规格是直径4cm),整理后的平均数和方差如下表,那么这四台机器生产的乒乓球既标准又稳定的是( )机器
甲
乙
丙
丁
平均数(单位:cm)
4.01
3.98
3.99
4.02
方差
0.03
2.4
1.1
0.3
A、甲 B、乙 C、丙 D、丁8. 共享单车为市民出行带来了方便,某单车公司第一季度投放1万辆单车,计划第三季度投放单车的数量比第一季度多4400辆,设该公司第二、三季度投放单车数量的平均增长率为x,则所列方程正确的是( )A、(1+x)2=4400 B、(1+x)2=1.44 C、10000(1+x)2=4400 D、10000(1+2x)=144009. 如图,在四边形ABCD中,AB=BC=2,且∠B=∠D=90°,连接AC,那么四边形ABCD的最大面积是( )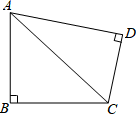 A、2 B、4 C、4 D、810. 如图,AC、BD是四边形ABCD的对角线,若E、F、G、H分别是BD、BC、AC、AD的中点,顺次连接E、F、G、H四点,得到四边形EFGH,则下列结论不正确的是( )
A、2 B、4 C、4 D、810. 如图,AC、BD是四边形ABCD的对角线,若E、F、G、H分别是BD、BC、AC、AD的中点,顺次连接E、F、G、H四点,得到四边形EFGH,则下列结论不正确的是( ) A、四边形EFGH一定是平行四边形 B、当AB=CD时,四边形EFGH是菱形 C、当AC⊥BD时,四边形EFGH是矩形 D、四边形EFGH可能是正方形
A、四边形EFGH一定是平行四边形 B、当AB=CD时,四边形EFGH是菱形 C、当AC⊥BD时,四边形EFGH是矩形 D、四边形EFGH可能是正方形二、填空题
-
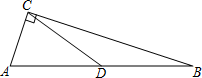
11. 比较大小:3223 .12. 数据2,0,1,9,0,6,1,6的中位数是 .13. 如图,点D是Rt△ABC斜边AB的中点,AC=8,CD=8.5,那么BC= .
 14. 关于x的一元二次方程(m-5)x2+2x+2=0有实根,则m的最大整数解是 .15. 《九章算术》是我国最重要的数学著作之一,其中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何”.译文大意是:“有一根竹子高一丈(十尺),竹梢部分折断,尖端落在地上,竹尖与竹根的距离三尺,问竹干还有多高”,若设未折断的竹干长为x尺,根据题意可列方程为 .
14. 关于x的一元二次方程(m-5)x2+2x+2=0有实根,则m的最大整数解是 .15. 《九章算术》是我国最重要的数学著作之一,其中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何”.译文大意是:“有一根竹子高一丈(十尺),竹梢部分折断,尖端落在地上,竹尖与竹根的距离三尺,问竹干还有多高”,若设未折断的竹干长为x尺,根据题意可列方程为 .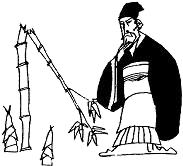 16. 如图,在矩形ABCD中,AB=6,AD=4,过矩形ABCD的对角线交点O作直线分别交CD、AB于点E、F,连接AE,若△AEF是等腰三角形,则DE= .
16. 如图,在矩形ABCD中,AB=6,AD=4,过矩形ABCD的对角线交点O作直线分别交CD、AB于点E、F,连接AE,若△AEF是等腰三角形,则DE= .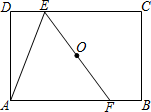
三、解答题
-
17. 计算: +18. 如图,在6×6的网格中,每个小正方形的边长为1,点A在格点(小正方形的顶点)上,试在各网格中画出顶点在格点上,面积为6,且符合相应条件的图形
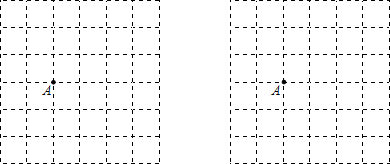 (1)、以A为顶点的平行四边形;(2)、以A为对角线交点的平行四边形.19. 已知在线段AB上有一点C(点C不与A、B重合且AC>BC),分别以AC、BC为边作正方形ACED和正方形BCFG,其中点F在边CE上,连接AG.
(1)、以A为顶点的平行四边形;(2)、以A为对角线交点的平行四边形.19. 已知在线段AB上有一点C(点C不与A、B重合且AC>BC),分别以AC、BC为边作正方形ACED和正方形BCFG,其中点F在边CE上,连接AG.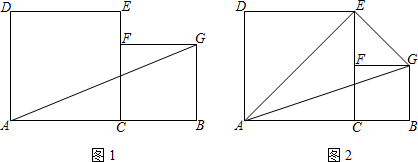 (1)、如图1,若AC=7,BC=5,则AG=;(2)、如图2,若点C是线段AB的三等分点,连接AE、EG,求证:△AEG是直角三角形.20. 为了了解同学们对垃圾分类知识的知晓程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校环保社团的同学们设计了“垃圾分类知识及投放情况”的问卷,并在本校随机抽取了若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部成绩分成A,B,C,D四组,并绘制了如下不完整的统计图表:
(1)、如图1,若AC=7,BC=5,则AG=;(2)、如图2,若点C是线段AB的三等分点,连接AE、EG,求证:△AEG是直角三角形.20. 为了了解同学们对垃圾分类知识的知晓程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识.某校环保社团的同学们设计了“垃圾分类知识及投放情况”的问卷,并在本校随机抽取了若干名同学进行了问卷测试,根据测试成绩分布情况,他们将全部成绩分成A,B,C,D四组,并绘制了如下不完整的统计图表:
组别
分数段
频数
频率
A
60≤x<70
a
b
B
70≤x<80
24
0.4
C
80≤x<90
18
c
D
90≤x<100
12
0.2
请根据上述统计图表,解答下列问题:
(1)、共抽取了多少名学生进行问卷测试?(2)、补全频数分布直方图;(3)、如果测试成绩不低于80分者为“优秀”,请你估计全校2000名学生中,“优秀”等次的学生约有多少人?21. 如图1,矩形ABCD中,AB=2,BC=3,过对角线AC中点O的直线分别交边BC、AD于点E、F (1)、求证:四边形AECF是平行四边形;(2)、如图2,当EF⊥AC时,求EF的长度.
(1)、求证:四边形AECF是平行四边形;(2)、如图2,当EF⊥AC时,求EF的长度.四、计算题(本大题共 2 小题,共 14 分)