安徽省合肥市庐阳区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期：2020-05-25 类型：期末考试
一、选择题
-
1. 下列根式是最简二次根式的是（ ）A、 B、 C、 D、2. 一元二次方程x2=x的根是（ ）A、x=0 B、x=1 C、x1=0，x2=1 D、无实根3.
用配方法解方程：x2-2x-3=0时，原方程变形为（ ）
A、（x+1）2=4 B、（x-1）2=4 C、（x+2）2=2 D、（x-2）2=34. 若正多边形的一个外角是 ，则该正多边形的内角和为（ ）A、 B、 C、 D、5. 共享单车为市民出行带来了方便，某单车公司第一个月投放1000辆单车，计划第三个月投放单车数量比第一个月多440辆．设该公司第二、三两个月投放单车数量的月平均增长率为x，则所列方程正确的为（ ）A、1000（1+x）2=1000+440 B、1000（1+x）2=440 C、440（1+x）2=1000 D、1000（1+2x）=1000+4406. 在Rt△ABC中，∠C=90°，AB=3，AC=2，则BC的值（ ）A、 B、 C、 D、7. 若关于x的一元二次方程bx2+2bx+4=0有两个相等的实数根，则b的值为（ ）A、0 B、4 C、0或4 D、0或-48. 某篮球队10名队员的年龄结构如表：年龄/岁
19
20
21
22
24
26
人数
1
1
x
y
2
1
已知该队队员年龄的中位数为21.5，则众数是（ ）
A、21岁 B、22岁 C、23岁 D、24岁9. 如图，延长矩形ABCD的边BC至点E，使CE=BD，连接AE，若∠ADB=40°，则∠E的度数是（ ）
A、20° B、25° C、30° D、35°10. 如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC=7，则MN的长度为（ ）
A、 B、2 C、 D、3二、填空题
-
11. 式子 在实数范围内有意义，则 x 的取值范围是 ．12. 如图，正方形ABCD的顶点C，A分别在x轴，y轴上，BC是菱形BDCE的对角线．若BC=6，BD=5，则点D的坐标是 ．
13. 已知m是一元二次方程x2-x-4=0的一个根，则代数式2+m-m2的值是 ．14. 在△ABC中，∠BAC=90°，AB=AC=4，O是BC的中点，D是腰AB上一点，把△DOB沿OD折叠得到△DOB′，当∠ADB′=45°时，BD的长度为 ．三、解答题（本大题共 7 小题，共 72 分）
-
15. 计算：（ - ）×216. 如图，在正方形网格中，每个小正方形的边长为1，△ABC为格点三角形（即A，B，C均为格点），求BC上的高．
17. 如图所示，在平行四边形ABCD中，AE、CF分别是∠DAB、∠BCD的平分线，求证：四边形AFCE是平行四边形．
18. 由中宣部建设的“学习强国”学习平台正式上线，这是推动习近平新时代中国特色社会主义思想，推进马克思主义学习型政党和学习型社会建设的创新举措．某校党组织随机抽取了部分党员教师某天的学习成绩进行了整理，分成5个小组（x表示成绩，单位：分，且20≤x＜70），根据学习积分绘制出部分频数分布表和部分频数分布直方图，其中第2，第5两组测试成绩人数直方图的高度比为3：1，请结合下列图表中相关数据回答下列问题：学习积分频数分布表
组别
成绩x分
频数
频率
1
20≤x＜30
5
2
30≤x＜40
b
3
40≤x＜50
15
30%
4
50≤x＜60
10
5
60≤x＜70
a
(1)、填空：a= ， b=；(2)、补全频数分布直方图；(3)、据统计，该校共有党员教师200人，请你估计每天学习成绩在40分以上的党员教师人数．19. 如图，矩形ABCD中，AB=4，BC=10，E在AD上，连接BE，CE，过点A作AG∥CE，分别交BC，BE于点G，F，连接DG交CE于点H．若AE=2，求证：四边形EFGH是矩形．
20. 一商品销售某种商品，平均每天可售出20件，每件盈利50元.为了扩大销售，增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.(1)、若每件商品降价2元，则平均每天可售出件；(2)、当每件商品降价多少元时，该商品每天的销售利润为1600元？21. 如图1，在正方形ABCD中，对角线AC，BD交于点O，点E在AB上，点F在BC的延长线上，且AE=CF．连接EF交AC于点P，分别连接DE，DF．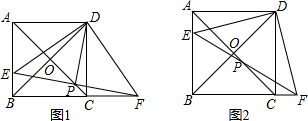
(1)、求证：△ADE≌△CDF；(2)、求证：PE=PF；(3)、如图2，若PE=BE，则 的值是 ． （直接写出结果即可）．四、计算题（本大题共 2 小题，共 18 分）