安徽省合肥市庐江县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-25 类型:期末考试
一、选择题
-
1. 要使式子 有意义,则x的取值范围是( )A、x>0 B、x≥-2 C、x≥2 D、x≤22. 判断下列三条线段a,b,c组成的三角形不是直角三角形的是( )A、a=4,b=5,c=3 B、a=7,b=25,c=24 C、a=40,b=50,c=60 D、a=5,b=12,c=133. 下列各式计算正确的是( )A、 + = B、2 - = C、 = × D、 ÷ =4. 已知n是正整数, 是整数,则n的最小值是( )A、1 B、2 C、3 D、45. 一次函数y=kx-b,当k<0,b<0时的图象大致位置是( )A、
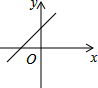 B、
B、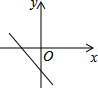 C、
C、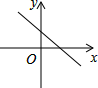 D、
D、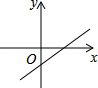 6. 11名同学参加数学竞赛初赛,他们的得分互不相同,按从高分录到低分的原则,取前6名同学参加复赛,现在小明同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的( )A、平均数 B、中位数 C、众数 D、方差7.
6. 11名同学参加数学竞赛初赛,他们的得分互不相同,按从高分录到低分的原则,取前6名同学参加复赛,现在小明同学已经知道自己的分数,如果他想知道自己能否进入复赛,那么还需知道所有参赛学生成绩的( )A、平均数 B、中位数 C、众数 D、方差7.如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
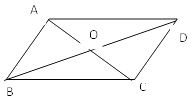 A、AB∥DC, AD∥BC B、AB∥DC, AD=BC C、AO=CO,BO=DO D、AB=DC,AD=BC8. 在平面直角坐标系中,把直线y=3x向左平移2个单位长度,平移后的直线解析式是( )A、y=3x+2 B、y=3x-2 C、y=3x+6 D、y=3x-69. 如图,已知两直线l1:y= x和l2:y=kx-5相交于点A(m,3),则不等式 x≥kx-5的解集为( )
A、AB∥DC, AD∥BC B、AB∥DC, AD=BC C、AO=CO,BO=DO D、AB=DC,AD=BC8. 在平面直角坐标系中,把直线y=3x向左平移2个单位长度,平移后的直线解析式是( )A、y=3x+2 B、y=3x-2 C、y=3x+6 D、y=3x-69. 如图,已知两直线l1:y= x和l2:y=kx-5相交于点A(m,3),则不等式 x≥kx-5的解集为( )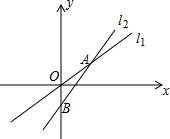 A、x≥6 B、x≤6 C、x≥3 D、x≤310. 如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A、x≥6 B、x≤6 C、x≥3 D、x≤310. 如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )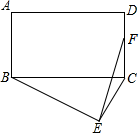 A、8 B、9 C、10 D、2
A、8 B、9 C、10 D、2二、填空题
-
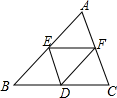
11. 一次函数y= - x,函数值y随x的增大而 .12. 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20+2 ,那么△DEF的周长是 .
 13. 如图,在平行四边形ABCD中,点E,F分别在边BC,AD上,请添加一个条件 , 使四边形AECF是平行四边形(只填一个即可).
13. 如图,在平行四边形ABCD中,点E,F分别在边BC,AD上,请添加一个条件 , 使四边形AECF是平行四边形(只填一个即可).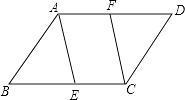 14. 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .
14. 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为 .
三、解答题
-
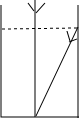
15. 计算(2 +1)(2 -1)-(1-2 )216. 在等边三角形ABC中,高AD=m,求等边三角形ABC的面积.17. 我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?
 18. 如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.
18. 如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.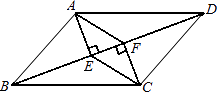 (1)、求证:△ABE≌△CDF;(2)、若AC与BD交于点O,求证:AO=CO.19. 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)、求证:△ABE≌△CDF;(2)、若AC与BD交于点O,求证:AO=CO.19. 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN. (1)、求证:四边形BMDN是菱形;(2)、若AB=4,AD=8,求MD的长.20. 某校八年级同学参加社会实践活动,到“庐江台湾农民创业园”了解大棚蔬菜生长情况.他们分两组对西红柿的长势进行观察测量,分别收集到10株西红柿的高度,记录如下(单位:厘米)
(1)、求证:四边形BMDN是菱形;(2)、若AB=4,AD=8,求MD的长.20. 某校八年级同学参加社会实践活动,到“庐江台湾农民创业园”了解大棚蔬菜生长情况.他们分两组对西红柿的长势进行观察测量,分别收集到10株西红柿的高度,记录如下(单位:厘米)第一组:32 39 45 55 60 54 60 28 56 41
第二组:51 56 44 46 40 53 37 47 50 46
根据以上数据,回答下列问题:
(1)、第一组这10株西红柿高度的平均数是 , 中位数是 , 众数是 .(2)、小明同学计算出第一组方差为S12=122.2,请你用计算器计算一下第二组方差,并说明哪一组西红柿长势比较整齐.21. 四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.这道题对大多数同学来说,印象深刻数学课代表在做完这题后,她把这题稍作改动,如图,四边形ABCD是正方形,点E是边BC的三等分点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,那么AE=EF还成立吗?如果成立,给予证明,如果不成立,请说明理由.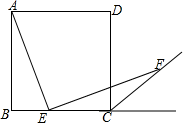 22. 如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
22. 如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.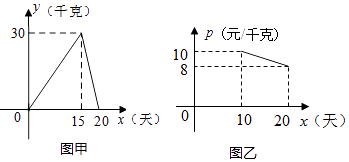 (1)、直接写出y与x之间的函数关系式;(2)、分别求出第10天和第15天的销售金额;(3)、若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?23. 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
(1)、直接写出y与x之间的函数关系式;(2)、分别求出第10天和第15天的销售金额;(3)、若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?23. 某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①→②→③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.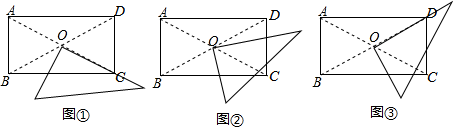 (1)、该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2 , 请你对这名成员在图①中发现的结论说明理由;(2)、在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.(3)、试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
(1)、该学习小组成员意外的发现图①中(三角板一边与CC重合),BN、CN、CD这三条线段之间存在一定的数量关系:CN2=BN2+CD2 , 请你对这名成员在图①中发现的结论说明理由;(2)、在图③中(三角板一直角边与OD重合),试探究图③中BN、CN、CD这三条线段之间的数量关系,直接写出你的结论.(3)、试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.