安徽省池州市石台县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2020-05-25 类型:期末考试
一、选择题(本大题共 10 小题,共 30 分)
-
1. 使 有意义的x的取值范围是( )A、x>3 B、x<3 C、x≥3 D、x≠32. 下列二次根式中能与2 合并的是( )A、 B、 C、 D、3. 一元二次方程y2-y- =0配方后可化为( )A、 =1 B、 =1 C、 = D、 =4. 一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x,则x满足( )A、16(1+2x)=25 B、25(1-2x)=16 C、16(1+x)2=2 D、25(1-x)2=165. 一个多边形内角和是1080°,则这个多边形是( )A、六边形 B、七边形 C、八边形 D、九边形6. 为考察两名实习工人的工作情况,质检部将他们工作第一周每天生产合格产品的个数整理成甲、乙两组数据,如下表:
甲
2
6
7
7
8
乙
2
3
4
8
8
关于以上数据,说法正确的是( )
A、甲、乙的众数相同 B、甲、乙的中位数相同 C、甲的平均数小于乙的平均数 D、甲的方差小于乙的方差7. 在一次酒会上,每两人都只碰一次杯,如果一共碰杯55次,则参加酒会的人数为( )A、9人 B、10人 C、11人 D、12人8. 如图,在正方形ABCD中,E在CD边上,F在BE边上,且AF=AB,过点F作FG⊥BE,交BC于点G,若CG=2,DE=7,则BE的长为( ) A、10 B、11 C、12 D、139. 如图,在菱形ABCD中,AC=6 ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
A、10 B、11 C、12 D、139. 如图,在菱形ABCD中,AC=6 ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )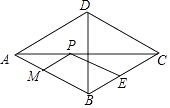 A、6 B、3 C、2 D、4.5
A、6 B、3 C、2 D、4.5二、填空题
-
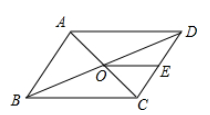
10. 已知0<a<2,化简:a+ = .11. 关于x的一元二次方程x2+3x-m=0有两个不相等的实数根,则实数m的取值范围是 .12. 如图▱ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE的周长为 .
 13. 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是 .
13. 在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是 .
三、解答题
-
14. 计算:50-(-2)+ × .15. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,顶端距离地面的高度AC为2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面的高度A′D为2米,求小巷的宽度.
 16. 随着移动互联网的快速发展,基于互联网的共享单车应运而生,为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.(1)、这组数据的中位数是 , 众数是 .(2)、计算这10位居民一周内使用共享单车的平均次数;(3)、若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数。17. 如图,在四边形ABCD中,AB=BC=CD,∠ABC+∠BCD=240°,
16. 随着移动互联网的快速发展,基于互联网的共享单车应运而生,为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.(1)、这组数据的中位数是 , 众数是 .(2)、计算这10位居民一周内使用共享单车的平均次数;(3)、若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数。17. 如图,在四边形ABCD中,AB=BC=CD,∠ABC+∠BCD=240°, (1)、利用尺规,以CD为边在四边形内部作等边△CDE(保留作图痕迹,不需要写作法)(2)、连接AE,判断四边形ABCE的形状,并说明理由.18. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价3元,则平均每天销售数量为件;(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?19. 如图①,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,点N为CM中点,CM的延长线交AB于点F,△DAE≌△CEM.
(1)、利用尺规,以CD为边在四边形内部作等边△CDE(保留作图痕迹,不需要写作法)(2)、连接AE,判断四边形ABCE的形状,并说明理由.18. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价3元,则平均每天销售数量为件;(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?19. 如图①,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,点N为CM中点,CM的延长线交AB于点F,△DAE≌△CEM.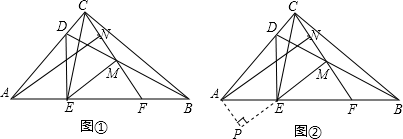 (1)、求证:CM=EM;(2)、求∠MEF的大小;(3)、如图②,过点A作AP⊥ME交ME的延长线于点P,求证:四边形ANMP为矩形.
(1)、求证:CM=EM;(2)、求∠MEF的大小;(3)、如图②,过点A作AP⊥ME交ME的延长线于点P,求证:四边形ANMP为矩形.四、计算题
-
20. 解方程:x2-2x-1=0.