安徽省池州市东至县2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-05-25 类型：期末考试

进入出卷网下载

一、选择题

1. 下列计算，正确的是（　　）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{\frac{1}{2}} = 2 \sqrt{2}$

查看试题解析
2. 若代数式 $\frac{\sqrt{x - 1}}{x - 2}$ 有意义，则实数x的取值范围是（　　）

A、x≥2 B、x≥1且x≠2 C、x＞l且x≠2 D、x≥1

查看试题解析
3. 若xy＜0，则 $\sqrt{x^{2} y}$ 化简后的结果是（）

A、 $x \sqrt{y}$ B、 $x \sqrt{- y}$ C、 $- x \sqrt{- y}$ D、 $- x \sqrt{y}$

查看试题解析
4. 一元二次方程x²-6x-5=0配方后可变形为（　　）

A、（x-3）²=14 B、（x-3）²=4 C、（x+3）²=14 D、（x+3）²=4

查看试题解析
5. 若关于x的一元二次方程（m-1）x²+5x+（m-1）（m-3）=0的常数项为0，则m的值等于（　　）

A、1 B、3 C、1或3 D、0

查看试题解析
6. 某班六名同学体能测试成绩（分）如下：80，90，75，75，80，80，对这组数据表述不正确的是（　　）

A、众数是80 B、方差是25 C、平均数是80 D、中位数是75

查看试题解析
7. 四边形ABCD中，AD=BC，BE=DF，AE⊥BD，CF⊥BD，垂足分别为E，F，则四边形ABCD一定是（　　）

A、正方形 B、菱形 C、平行四边形 D、矩形

查看试题解析
8. 如图所示，四边形OABC为正方形，边长为3，点A、C分别在x轴，y轴的正半轴上，点D在OA上，且D点的坐标为（1，0），P是OB上的一个动点，则PD+PA和的最小值是（　　）

A、2 $\sqrt{10}$ B、 $\sqrt{10}$ C、4 D、9

查看试题解析
9. 如图，正方形ABCD的边长为10，AG=CH=8，BG=DH=6，连接GH，则线段GH的长为（　　）

A、 $\frac{8 \sqrt{3}}{5}$ B、2 $\sqrt{2}$ C、 $\frac{14}{5}$ D、10-5 $\sqrt{2}$

查看试题解析
10. 如图，在正方形ABCD中，AC、BD相交于点O，E、F分别为BC、CD上的两点，BE＝CF，AE、BF分别交BD、AC于M、N两点，连OE、OF．下列结论：①AE＝BF；②AE⊥BF；③CE+CF＝BD；④S_{四边形OECF}＝ $\frac{1}{4}$ S_{正方形ABCD} ，其中正确的是（）

A、①② B、①④ C、①②④ D、①②③④

查看试题解析

二、填空题

11. 若 $\sqrt{8}$ 与最简二次根式 $\sqrt{a}$ 是同类二次根式，则a= ．

查看试题解析
12. 若a= $\frac{2}{\sqrt{3} - 1}$ ，则 $\frac{1}{2} a^{3} - a^{2} - a + 2$ = ．

查看试题解析
13. 关于x的两个方程x²-x-2=0与 $\frac{1}{x + 1} = \frac{2}{x + a}$ 有一个解相同，则a= ．

查看试题解析
14. 若一个三角形的三边的比为3：4：5，则这个三角形的三边上的高之比为．

查看试题解析
15. 观察分析下列数据：0，- $\sqrt{3}$ ， $\sqrt{6}$ ，-3，2 $\sqrt{3}$ ，- $\sqrt{15}$ ，3 $\sqrt{2}$ ，…，根据数据排列的规律得到第13个数据应是．

查看试题解析
16.
用4个全等的正八边形进行拼接，使相等的两个正八边形有一条公共边，围成一圈后中间形成一个正方形，如图1，用n个全等的正六边形按这种方式进行拼接，如图2，若围成一圈后中间形成一个正多边形，则n的值为．

查看试题解析
17. 如图，点O是▱ABCD的对角线交点，AD＞AB，E、F是AB边上的点，且EF= $\frac{1}{2}$ AB；G、H是BC边上的点，且GH= $\frac{1}{3}$ BC，若S₁ ， S₂分别表示△EOF和△GOH的面积，则S₁：S₂= ．

查看试题解析
18. 如图，在矩形ABCD中，AD=5，AB=8，点E为射线DC上一个动点，把△ADE沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为．

查看试题解析

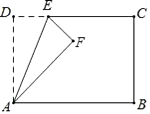
三、解答题

19. 计算：（ $\sqrt{5}$ -2）（2+ $\sqrt{5}$ ）-（- $\sqrt{3}$ ）²+ $\sqrt{8}$ ÷ $\sqrt{2}$ ．

查看试题解析
20. 解方程：（x+1）（2x-6）=1

查看试题解析
21. 已知关于x的一元二次方程（m-2）x²+2mx+m+3=0有两个不相等的实数根．

(1)、求m的取值范围；

(2)、当m取满足条件的最大整数时，求方程的根．

查看试题解析
22. 在△ABC中，E是AC边上一点，线段BE垂直∠BAC的平分线于D点，点M为BC边的中点，连接DM．

(1)、求证：DM= $\frac{1}{2}$ CE；

(2)、若AD=6，BD=8，DM=2，求AC的长．

查看试题解析
23. 2014年1月，国家发改委出台指导意见，要求2015年底前，所有城市原则上全面实行居民阶梯水价制度，小明为了解市政府调整水价方案的社会反响，随机访问了自己居住小区的部分居民，就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查，并把调查结果整理成下面的图1，图2．

小明发现每月每户的用水量在5m³-35m³之间，有8户居民对用水价格调价涨幅抱无所谓，不会考虑用水方式的改变，根据小明绘制的图表和发现的信息，完成下列问题：

(1)、n= ，小明调查了户居民，并补全图1；

(2)、每月每户用水量的中位数和众数分别落在什么范围？

(3)、如果小明所在小区有1800户居民，请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少．

查看试题解析
24. 某商店以每件50元的价格购进某种品牌衬衫100件，为使这批衬衫尽快出售，该商店先将进价提高到原来的2倍，共销售了10件，再降低相同的百分率作二次降价处理；第一次降价标出了“出厂价”，共销售了40件，第二次降价标出“亏本价”，结果一抢而光，以“亏本价”销售时，每件衬衫仍有14元的利润．

(1)、求每次降价的百分率；

(2)、在这次销售活动中商店获得多少利润？请通过计算加以说明．

查看试题解析
25. 如图（1），在矩形ABCD中，M、N分别是AB、CD的中点，作射线MN，连接MD、MC

(1)、请直接写出线段MD与MC的数量关系；

(2)、将矩形ABCD变为平行四边形，其中∠A为锐角，如图（2），AB=2BC，M、N分别是AB、CD的中点，过点C作CE⊥AD交射线AD于点E，交射线MN于点F，连接ME、MC，求证：ME=MC；

(3)、写出∠BME与∠AEM的数量关系，并证明你的结论．

查看试题解析