安徽省安庆市潜山市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2020-05-25 类型：期末考试

进入出卷网下载

一、选择题

1. 下列各式中的最简二次根式是（　　）

A、 $\sqrt[3]{a}$ B、 $\sqrt{2 a^{2}}$ C、 $\frac{1}{2} \sqrt{a}$ D、 $\sqrt{\frac{1}{a}}$

查看试题解析
2. 下列方程是关于x的一元二次方程的是（　　）

A、ax²+bx+c=0 B、x+ $\frac{1}{x}$ =2 C、（x-1）（x+1）=0 D、3x²+4xy-y²=0

查看试题解析
3. 某电子产品经过连续两次降价，售价由4900元降到了3600元．设平均每月降价的百分率为x，根据题意列出的方程是（　　）

A、4900（1+x）²=3600 B、4900（1-x）²=3600 C、4900（1-2x）²=3600 D、3900（1-x）²=4900

查看试题解析
4. 依次连接四边形ABCD各边的中点所得四边形是矩形，则四边形ABCD一定是（　　）

A、菱形 B、对角线相等的四边形 C、矩形 D、对角线互相垂直的四边形

查看试题解析
5.
如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为（）

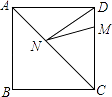A、6 B、8 C、12 D、10

查看试题解析
6. 如图所示，已知四边形ABCD是平行四边形，下列结论中，不一定正确的是（　　）

A、△AOB的面积等于△AOD的面积 B、当AC⊥BD时，它是菱形 C、当OA=OB时，它是矩形 D、△AOB的周长等于△AOD的周长

查看试题解析
7. 设直角三角形的两条直角边长及斜边上的高分别为a，b及h，则下列关系正确的是（）

A、 $\frac{1}{a^{2}} + \frac{1}{b^{2}} = \frac{1}{h^{2}}$ B、 $\frac{1}{a} + \frac{1}{h} = \frac{1}{b}$ C、 $\frac{1}{b^{2}} + \frac{1}{h^{2}} = \frac{1}{a^{2}}$ D、 $\frac{1}{a} + \frac{1}{b} = \frac{1}{h}$

查看试题解析
8. 如图是一张月历表，在此月历表上用一个长方形任意圈出2×2个数（如17，18，24，25），如果圈出的四个数中最小数与最大数的积为153，那么这四个数的和为（　　）

A、40 B、48 C、52 D、56

查看试题解析
9. 为了解我市初三女生的体能状况，从某校初三的甲、乙两班各抽取27名女生进行一分钟跳绳次数测试，测试数据统计结果如下表，如果每分钟跳绳次数≥105次的为优秀，那么甲、乙两班的优秀率的关系是（　　）

班级

人数

中位数

平均数

甲班

27

104

97

乙班

27

106

96

A、甲_优＜乙_优 B、甲_优＞乙_优 C、甲_优=乙_优 D、无法比较

查看试题解析
10. 如图是按一定规律排成的三角形数阵，按图中数阵的排列规律，第10行从左至右第6个数是（　　）

A、2 $\sqrt{10}$ B、 $\sqrt{41}$ C、5 $\sqrt{2}$ D、 $\sqrt{51}$

查看试题解析

二、填空题

11. 已知a＜b，化简二次根式 $\sqrt{- a^{3} b}$ 的正确结果是．

查看试题解析
12. 在市业余歌手大奖赛的决赛中，参加比赛的10名选手成绩统计如图所示，则这10名选手成绩的中位数是．

查看试题解析
13. 在矩形ABCD中，AB=4，对角线AC，BD相交于点O，AE垂直平分OB于点E，则AD的长为．

查看试题解析
14. 在等腰△ABC中，三边分别为a、b、c，其中a=4，b、c恰好是方程x²-（2k+1）x+5（k- $\frac{3}{4}$ ）=0的两个实数根，则△ABC的周长为．

查看试题解析
15. 如图是由16个边长为1的正方形拼成的图案，任意连结这些小格点的三个顶点可得到一些三角形．与A，B点构成直角三角形ABC的顶点C的位置有个．

查看试题解析
16. 如图，四边形ABCD沿直线AC对折后重合，如果AC，BD交于O，AB∥CD，则结论①AB=CD，②AD∥BC，③AC⊥BD，④AO=CO，⑤AB⊥BC，其中正确的结论是（填序号）．

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{18}$ -2 $\sqrt{\frac{1}{2}}$ - $\sqrt{2}$ （2- $\sqrt{2}$ ）；

(2)、 $\frac{2}{3} \sqrt{9 x}$ -6 $\sqrt{\frac{x}{4}}$ +2x $\sqrt{\frac{1}{x}}$ ．

查看试题解析
18. 为弘扬中华传统文化，某学校决定开设民族器乐选修课．为了更贴合学生的兴趣，对学生最喜爱的一种民族乐器进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：

(1)、在这次抽样调查中，共调查名学生；

(2)、请把条形图（图1）补充完整；

(3)、求扇形统计图（图2）中，二胡部分所对应的圆心角的度数；

(4)、如果该校共有学生1500名，请你估计最喜爱古琴的学生人数．

查看试题解析
19. 银隆百货大楼服装柜在销售中发现：“COCOTREE”牌童装每件成本60元，现以每件100元销售，平均每天可售出20件．为了迎接“五•一”劳动节，商场决定采取适当的降价措施，以扩大销售量，增加盈利，尽量减少库存．经市场调查发现：如果每件童装降价1元，那么平均每天就可多销售2件．

(1)、要想平均每天销售这种童装盈利1200元，请你帮商场算一算，每件童装应定价多少元？

(2)、这次降价活动中，1200元是最高日利润吗？若是，请说明理由；若不是，请试求最高利润值．

查看试题解析
20.
如图，在Rt△ABC中，∠B=90°，BC=5 $\sqrt{3}$ ，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．

(1)、AC的长是， AB的长是．

(2)、在D、E的运动过程中，线段EF与AD的关系是否发生变化？若不变化，那么线段EF与AD是何关系，并给予证明；若变化，请说明理由．

(3)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．

(4)、当t为何值，△BEF的面积是2 $\sqrt{3}$ ？

查看试题解析
21. 如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA、OB的长分别是一元二次方程x²-9x+20=0的两个根（OA＞OB）．

(1)、求点D的坐标；

(2)、求直线BC的解析式；

(3)、在直线BC上是否存在点P，使△PCD为等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由．

查看试题解析

四、计算题（本大题共2小题，共16分）

22. 解下列方程

(1)、 $\frac{1}{2}$ x²+x=2（配方法）；

(2)、2x²-7x+6=0（公式法）．

查看试题解析
23. 如图，O是矩形ABCD对角线的交点，DE∥AC，CE∥BD．

(1)、求证：四边形OCED是菱形；

(2)、若∠AOD=120°，DE=3，求矩形ABCD的面积．

查看试题解析

班级	人数	中位数	平均数
甲班	27	104	97
乙班	27	106	96