浙江省宁波市慈溪市六校2018-2019学年高二下学期数学期中联考试卷
试卷更新日期:2020-05-25 类型:期中考试
一、单选题
-
1. 已知 为虚数单位,则 在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 6把椅子摆成一排,3人随机就座,任何两人不相邻的坐法种数为( )A、144 B、120 C、72 D、243. 若 ,则 的值为( )A、4 B、4或5 C、6 D、4或64. 设 ,则 的递减区间为( ).A、 B、 C、 , D、5. 用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为 ( )A、324 B、328 C、360 D、6486. 用反证法证明“已知 ,求证: .”时,应假设( )A、 B、 C、 且 D、 或7. 将5种不同的花卉种植在如图所示的四个区域中,每个区域种植一种花卉,且相邻区域花卉不同,则不同的种植方法种数是( ).
 A、420 B、180 C、64 D、258. 已知 ,若对任意两个不等的正实数 , ,都有 恒成立,则a的取值范围是( )A、 B、 C、 D、9. 如图所示,在著名的汉诺塔问题中,有三根高度相同的柱子和一些大小及颜色各不相同的圆盘,三根柱子分别为起始柱、辅助柱及目标柱.已知起始柱上套有 个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为 ,则 ( )
A、420 B、180 C、64 D、258. 已知 ,若对任意两个不等的正实数 , ,都有 恒成立,则a的取值范围是( )A、 B、 C、 D、9. 如图所示,在著名的汉诺塔问题中,有三根高度相同的柱子和一些大小及颜色各不相同的圆盘,三根柱子分别为起始柱、辅助柱及目标柱.已知起始柱上套有 个圆盘,较大的圆盘都在较小的圆盘下面.现把圆盘从起始柱全部移到目标柱上,规则如下:每次只能移动一个圆盘,且每次移动后,每根柱上较大的圆盘不能放在较小的圆盘上面,规定一个圆盘从任一根柱上移动到另一根柱上为一次移动.若将 个圆盘从起始柱移动到目标柱上最少需要移动的次数记为 ,则 ( )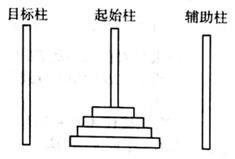 A、33 B、31 C、17 D、1510. 定义在 上的可导函数 ,当 时, 恒成立, ,则 的大小关系为 ( )A、 B、 C、 D、
A、33 B、31 C、17 D、1510. 定义在 上的可导函数 ,当 时, 恒成立, ,则 的大小关系为 ( )A、 B、 C、 D、二、双空题
-
11. 在如图所示的 的方格纸上(每个小方格均为正方形),共有个矩形、个正方形.12. 若复数 (i是虚数单位),则z的虚部为 , .13. 实数 满足:对任意 ,都有 ,则 , .14. 已知函数 .若函数在 上是单调函数,则实数 的取值范围是;若函数在 上是增函数,则实数 的取值范围是 .
三、填空题
-
15. 函数 的导函数为 .16. 用数学归纳法证明“ ”时,由 不等式成立,推证 时,则不等式左边增加的项数共项17. 将5名上海世博会的志愿者分配到中国馆、美国馆、英国馆工作,要求每个国家馆至少分配一名志愿者且其中甲、乙两名志愿者不同时在同一个国家馆工作,则不同的分配方案有种.
四、解答题
-
18. 已知函数 .
(Ⅰ)求曲线 在点 处的切线方程;
(Ⅱ)直线 为曲线 的切线,且经过原点,求直线 的方程及切点坐标.
19. 在 的展开式中,第4项的系数与倒数第4项的系数之比为 .(1)、求 的值;(2)、求展开式中所有的有理项;(3)、求展开式中系数最大的项.20. 已知函数 .(I)求f(x)的极小值和极大值;
(II)当曲线y = f(x)的切线 的斜率为负数时,求 在x轴上截距的取值范围.